The Essence of NN 神经网络的本质
写这篇文章的动机: To record and share the mental framework of ML personally. This framework is self-contained but I will quote later content even in the first chapter. Remember, one CANNOT ever learn anything just by reading any article from the top to the bottom and stopped once stucked.
This blog is under construction!
Change of Mind
I don’t think view neural networks as black boxes does any help towards understanding and inventing new networks.
对一个神经网络来说, 我们要站在它的角度考虑 up to what extend it could tell the difference of data? 比如图像处理的神经网络, 它肯定不知道输入的是一张图, 如果是一段文字呢? 如果对于很多类型的数据它都不能区分, 说明这个网络非常 general 但性能肯定很差.
I don’t see any advantages to view a NN as a black box!
Questions
梯度下降和反向传播的关系是什么?
我们算梯度是在什么空间里面?
梯度下降在 Transformer 里面是如何工作的?
Neural Network is Not So Different
目标: 找一个映射.
Frame Every Problem as a Mapping
运用 NN 解决问题的第一步就是将你的问题用一个映射来描述, 然后让计算机找这个映射. 这个映射还不是数学上那种精确的映射, 会有很多额外的问题需要考虑:
每个输入都需要有结果输出吗? 肯定不是的, 比如你给计算机一段随机文字让它续写, 它可以有输出, 但是我们肯定期望它给出一个「您给我的文字我看不懂」的回答嘛.
我们希望它每次输出的答案都不太一样, 比如每次续写一段故事. 所以这个映射一般也会要求要有随机性.
给计算机多少信息呢? 这一步很关键!
- 给的信息少了或者无关的信息效果肯定差, 比如你在没有任何先验的情况下告诉计算机你的性别, 要求它给你期末考试的答案. 有时候你甚至不知道你给的信息少没少. 比如在 This Video 中: 你有一个每天会给你做饭的朋友, 他按照一定规律每天给你做 \(A, B, C\) 三种食物中的一个. 你觉得它跟星期几、月份和你朋友的心情有关, 你搭建了一个 \(3\) 输入 \(3\) 输出的神经网络每天用历史数据训练. 但是实际上他只是按照 \(A\to B\to C\to A\to \cdots\) 的顺序给你做的, 只是你太傻没注意到, 也没将制作的时间输入给神经网络, 网络永远学不到这个规律! (这是 RNN, LSTM 出现的动机之一)
- 但其实你永远也给不出全部的信息和无比精确的问题描述! 比如你让计算机续写文字, 续写多少字呢? 用什么语言? 需要符合逻辑吗? 甚至什么是续写? 这些永远也给不出精确的描述. 我们希望计算机默认地理解这些东西.
以什么样的存储形式喂给计算机数据呢? (Vector 和 Tensor 出现的动机)
Communicate with Computer
把你知道的东西通过某种方式告诉计算机, that’s it.
世界上很多问题其实就是一个复杂的映射, 比如图像识别就是输入是图片, 输出是图片中的各种内容. 只不过这个函数存在于人类的大脑中, 无法写出显式的表达式. 人类想要强行把这个函数的表达式找到! 怎么找呢? 我们看到一棵树, 它为什么是一棵树呢? 每个像素都对它是一棵树做出了贡献, 但好像整体是一棵树又与单个像素毫无关系. 如果这个表达式存在, 那么它肯定非常复杂 (这里不能追求所谓的 “简洁与优美”). 但我们可以缩小一点范围, 用某种特定形式的函数来逼近所求. 也就是:
在一堆某种形式的映射里面 (参数化的函数空间 \(\mathcal{\hat{F}}\)) 找到一个映射 \(\hat{f}\) 来拟合一个复杂的映射 \(f: \mathcal{X}\to \mathcal{Y}\)
人们首先发现长成 Equation eq-fcnn 这种样子的映射仿佛有很强的拟合能力, 也就是不管你人脑中的模型有多复杂, 总是可以在下面形式的映射中找到合适的拟合.
\[ \hat{f}(x) = \sigma (W^{[L]} \cdots \sigma (W^{[2]} \sigma (W^{[1]} x + b^{[1]}) + b^{[2]}) + \cdots + b^{[L]}) \tag{1}\]
Equation eq-fcnn 很复杂对吧. 但是它可以用下面的图可视化出来:
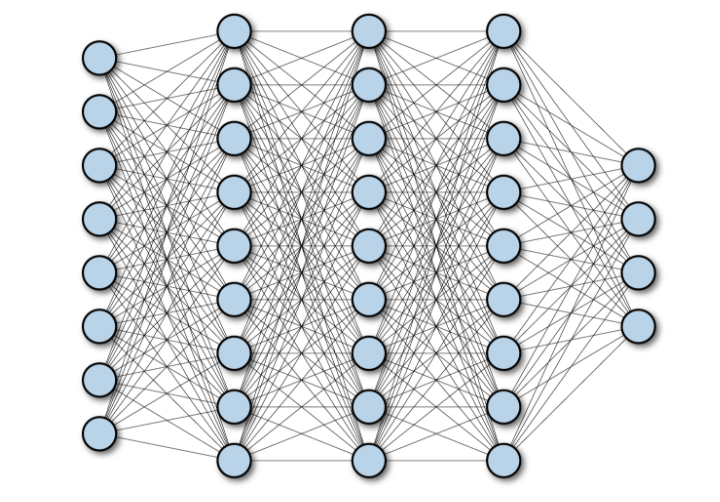
这张图放在这里太 cliché 了, 但是我想说的是: 我们对它太过熟悉了, 以至于认为选择这种参数化方法是理所应当、独一无二的.
(FCNN, CNN, Transformer是同一层面上的概念? FCNN 能做到的事情很多, 但是太general 了, 所以先猜测什么样的结构能更好地揭示规律 (比如卷积 (尊重了 \(\mathcal{X}\) 结构从而很可能能加速神经网络发现规律的过程?), 再比如 GNN), 然后加入它们来 帮助神经网络发现规律? “Differential Model” 我感觉 FCNN 和 CNN 的本质是一样的? CNN 的本质是 pre-trained FCNN (或者说?))
事实证明形如神经网络的那些参数化函数空间能够拟合绝大多数的复杂映射, 所以无脑选择这样的 \(\mathcal{\hat{F}}\) 就行了.
如果一个问题可以用以下的框架里面描述, 那么这个问题就可以用神经网络来解决!
「复杂的映射」
「复杂的映射」这个思想可以刻画和描述所有以下问题:
- Classification 分类问题: \(\mathcal{Y}\) 仅仅是没有任何结构的集合.
- 请说出下面例子的 \(\mathcal{X}\) 和 \(\mathcal{Y}\):
- Image Classification: 输入一张图片, 判断是猫还是狗还是其它的.
- Face Detection: 输入一张图片, 判断有没有人脸.
- Handwriting Recognition: 输入一张手写的数字, 判断是几. (虽然 \(\mathcal{Y}\) 有序结构, 但不关心)
- \(\mathcal{X}\) 是所有图片的集合, \(\mathcal{Y}\) 是所有类别的集合.
- 请说出下面例子的 \(\mathcal{X}\) 和 \(\mathcal{Y}\):
- Regression 回归问题: \(\mathcal{Y}\) 有序结构. (Generally speaking, 有拓扑结构1)
- 请说出下面例子 [1] 的 \(\mathcal{X}\) 和 \(\mathcal{Y}\):
- Linear Regression: 给定一个标量场, 用线性标量场来拟合. (相当于指定了 \(\mathcal{\hat{F}}\))
- Quantization: 根据市场情况、历史数据等, 预测明天的股票价格.
- 预测某个视频观看者年龄.
- 根据发送的控制信号, 预测机械臂在三维空间的坐标.
- 根据历史湿度、温度等天气信息, 预测某地明天的温度.
- 请说出下面例子 [1] 的 \(\mathcal{X}\) 和 \(\mathcal{Y}\):
1 序结构诱导的拓扑称为 Alexandrov 拓扑.
Sequence Models
TODO
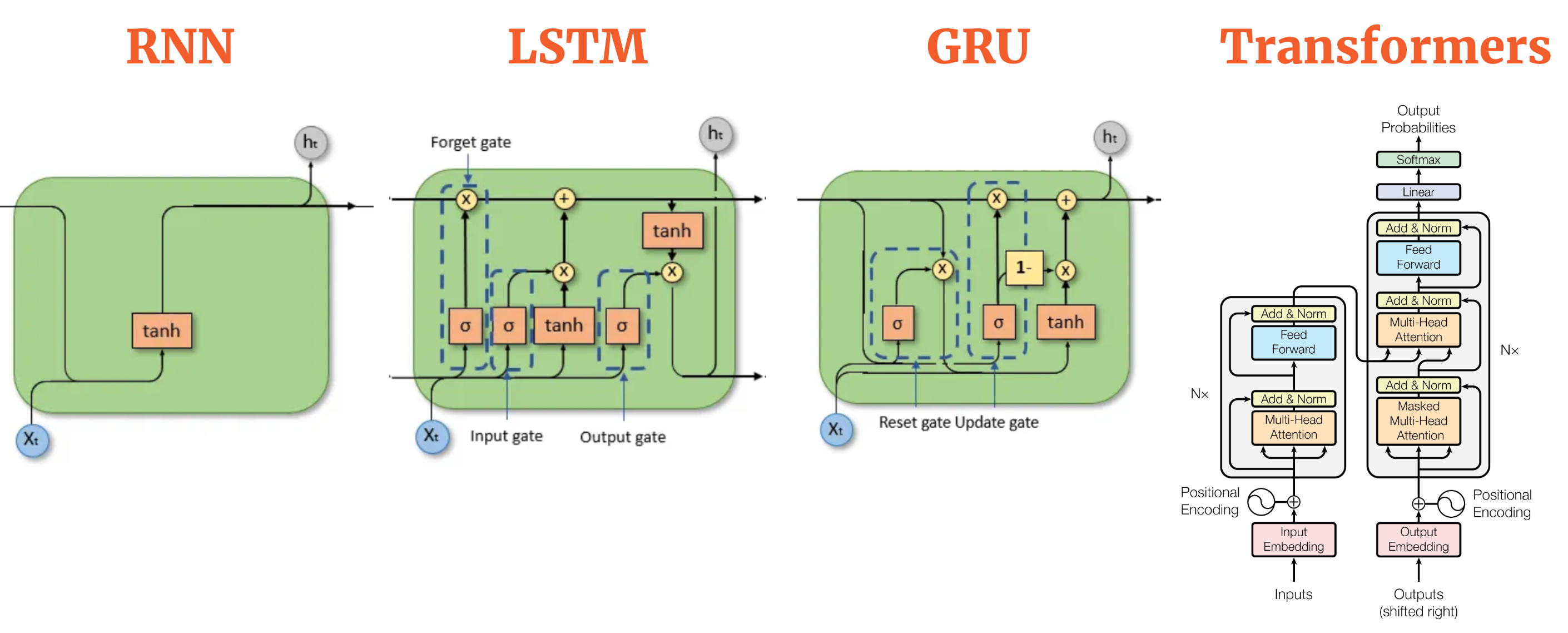
Design the Network
设想计算机可能会如何思考这个问题, 比如它需要记忆吗? 它需要关注上下文吗 (Transformer)? 然后设计出网络结构.
如果一个函数空间的所有元素都能用形式上相同的式子表达 (这个式子里面有一些可变的参数), 那么这个函数空间就是参数化的.
Linear Regression 的参数化函数空间同构2于 \(\mathbb{R}^2\):
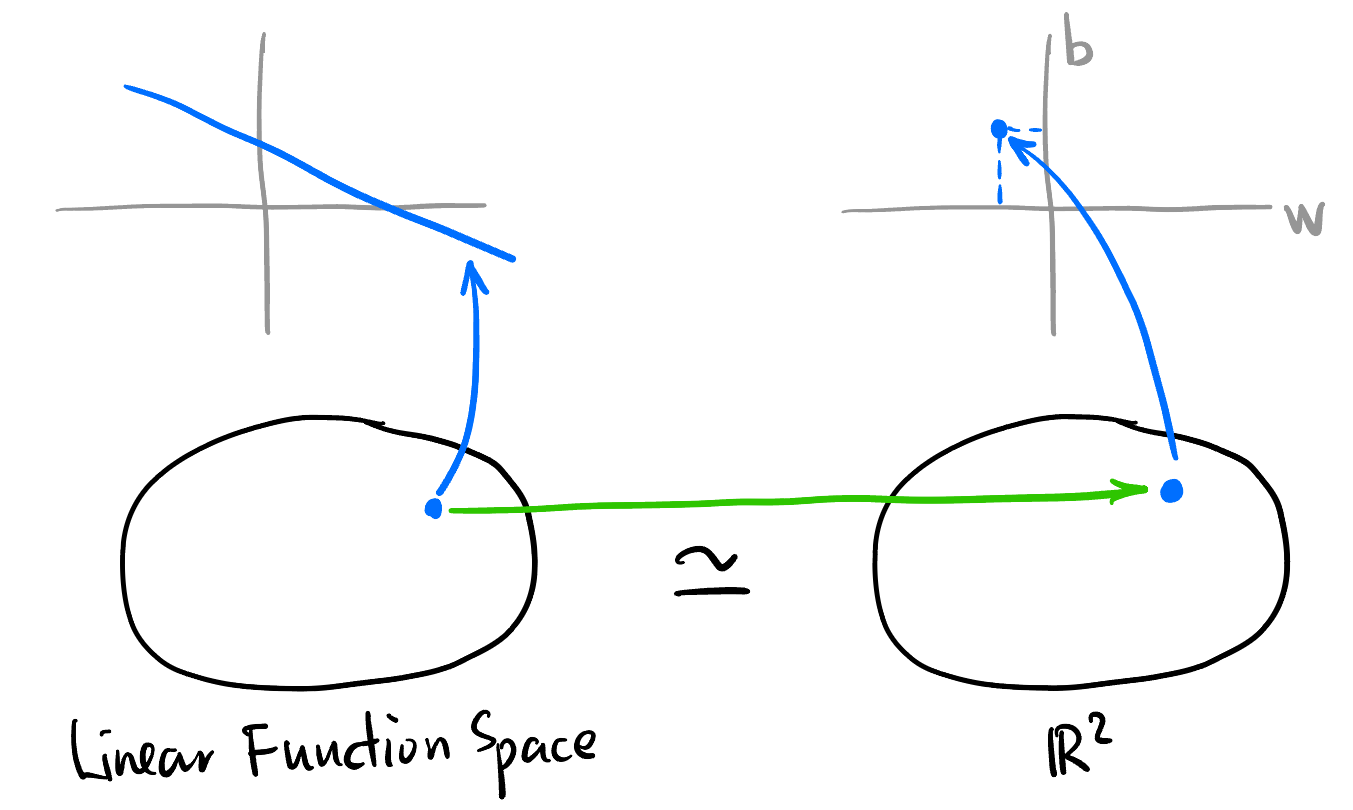
同构的 Mental picture
2 在拓扑向量空间的意义上: \[\{f: \mathbb{R}\to \mathbb{R} \mid f(x) = wx + b, w, b \in \mathbb{R}\} \simeq \{(w, b) \mid w, b \in \mathbb{R}\}\]
- 某个 CNN 的参数化函数空间同构于 \(\mathbb{R}^{200}\):
尊重 \(\mathcal{X}, \mathcal{Y}\) 中元素的结构
(升维、ask a lot of binary questions、编解码器、激活函数用什么类型 这些的联系是什么?)
(\(\mathcal{X}\) 为图片集合、文字、电路板、声音时分别有什么结构?)
(curse of dimension怎么解决?)
如果 \(\mathcal{X}\) 是一张图片的话, 我们有 “相邻” 点这种概念, 也就是说输入进 \(\hat{f}\) 的对象内部是有某些结构的, 但是 FCNN (a.k.a., MLP) 并不知道这些结构.
(引出 CNN 和 GNN)
Train the Network
(梯度下降, 各种优化器)
(梯度消失问题怎么解决、正则化、ResNet, 为什么ResNet有效等等话题)
Gradient Descent 梯度下降
- Loss function 损失函数: 函数空间 \(\mathcal{\hat{F}}\) 映到 \(\mathbb{R}\) 的标量场 \(L: \mathcal{\hat{F}} \to \mathbb{R}\), 由于 \(\mathcal{\hat{F}}\) 参数化, 所以 \(L\) 也可以看作是 \(\mathbb{R}^n \to \mathbb{R}\) 的函数.
- \(L\) 标量场如何确定呢?
- 用训练集中的所有样本点取平均来确定标量场 (“GD”, 计算量太大).
- 通过 (不放回地) 抽取训练集中的一个 Mini batch 来估计标量场 (“SGD / Minibatch SGD”)
- \(L\) 标量场如何确定呢?
torch.optim其它优化器:- Momentum: 通过加入历史速度来模拟惯性 (Moving Average), 受噪声影响更小.
- AdaGrad(Adaptive Gradient Descent)
- 一些参数
- Learning Rate 学习率
杂项
我发现要以线性的顺序来写这篇 blog 的话会增加很多不必要的复杂性, 所以接下来我直接按照本人的学习顺序进行整理.
CNN Padding:
为了解决输入输出大小不一致的问题, 可以引入 Padding.

不同的 Padding, Pytorch 的默认为 zero padding (最常用 [3]) 要将各种问题设计成用机器学习的方法的 idea 非常重要. 它往往是一篇论文的核心 idea. 比如 word2vec 中提到的方法.
一个网络结构最初可能是为了解决某个具体问题而设计的, 但是它往往可以被推广到其它完全不同的问题上 (比如图像分类和文本生成、encoder only, etc. (TBD)).
一些本人的看法, 先起名字封装起来, 方便以后复用:
- 「降临派」(The Adventists): 人类已经不能靠自身的力量解决问题了, 需要一个全知全能的存在来拯救人类, 而 AI 正是「降临派」正在构建的上帝, 然而目前来看:
- 「巴别塔工程」 [4]: 人类设计 AI 这个「上帝」的过程 (即设计神经网络的过程) 非常的 ad hoc, 从 LSTM, Transformer 的 \(QKV\), MoE, etc., 人类试图通过分析自身如何理解文字和图像, 或者揣测计算机有可能可以如何理解文字和图像 (“Inductive Bias” [5]), 设计出一些不具美感、结构复杂拙劣的网络结构 (后文称「巴别塔上的砖块」) 来表征这个思考过程, 试图构建他们畅想的上帝. 经过几个月的训练后, 巴别塔上又叠了一个新的砖块, 比所有的 benchmark 都高了 \(1.3\%\), 最终可以在论文里面用抽象的数学符号装 13, 不用人话甚至直接隐藏设计这些结构的动机和思维轨迹, 以至于后来的人花费大量时间去揣摩作者拍脑袋的成果 (后文称为「语言不通的巴比伦人」). 总之, 我对目前降临派的 AI 研究方法持有很深的怀疑态度 (后文称为「不存在的巴别塔」) [6].
如何看待机器学习领域论文?
- 「巴别塔」上的每一个砖块都是作者 2 分钟的灵光乍现 + 1 个月的史山产出 + 3 个月的调参训练 辛苦得出的结果. 设想一下, 如果有一个预言家女巫能够在你的 idea 刚刚冒出来的时候就告诉你它的性能, 并且你每给出一组 multi-head 的数量就告诉你性能变化 (毕竟这都是确定可以实现的事了), 你还觉得 AI 论文和 transformer 结构是多么神圣伟大吗? 但是每个砖块的性能都必须经历训练和调参的过程, 而并不能直接数学推导出它的性能. 所以从某种角度讲, AI 论文就是一个无数搬砖者花时间精力构建的「查找表」, 它告诉你: “这种形状的砖性能是这样的, 如果你有类似形状的砖块, 我已经给你研究过了.” 你自己如何看待这些砖块, 以及它们如何带给你一些 insights, 这取决于你自己.
CNN
TBD TBD TBD!
Transformer
- 一个 Attention head 里面的 Inductive Bias 分析:
- Query \(Q\): Hey, do you all have anything relevant in terms of <syntax> for me?
- Key \(K\): Here is what I can offer in terms of <syntax>.
- Score: How relevant is what you guys offer in terms of <syntax>?
- Value \(V\): What direction in the embedding space should I move to capture <syntax> information?
- Multi-head: 相当于问很多个不同的问题, 即改变 “<>” 里面的内容, 比如 <meaning>, <irrelevance>, <description>, etc.
- 合并多个 head 输出的向量可以用相加或者拼接.
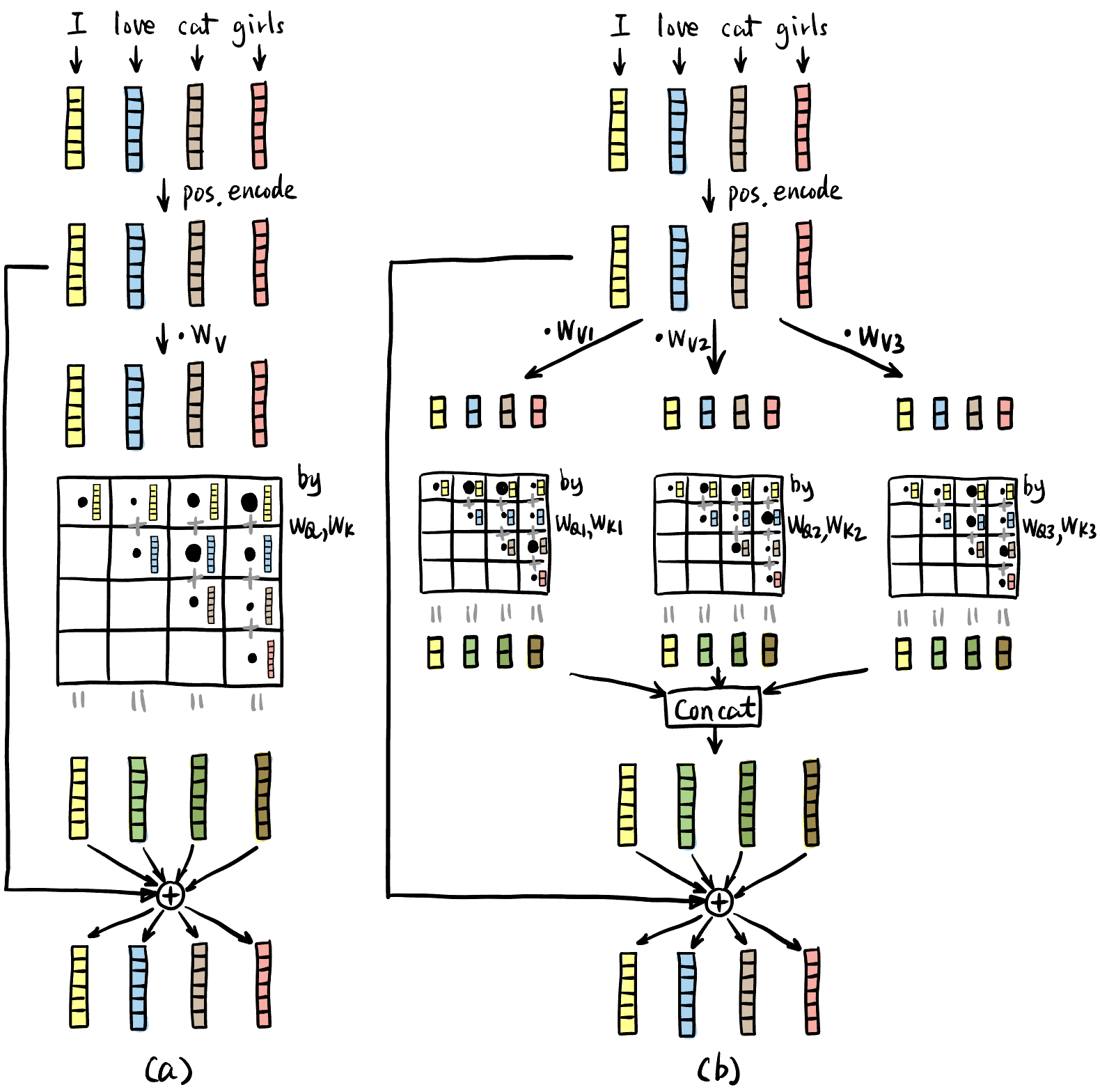
Figure 3: (a) Single Head Attention; (b) 3-head Attention. ( dim = 6,dim_head = 2,heads = 3,inner_dim = 2*3 = 6 = dim)