ML Infra 基础

Tensor 张量

  • 动机: 很多地位都相同的数据可以用一维数组存储. 如果有很多不同「地位」的数据, 我们给没种地位分配一个维度来存储, 这就是张量.

  • 名字来源: 由于数学里 \((0,k)\)-tensor \(T: V^k \to \mathbb{F}\) 在选取一组 basis \(\{\mathbf{e}_i\}_{i=1}^k\) 后的 representation 刚好是一个 \(k\) 维数组 \(T_{i_1i_2 \cdots i_k}\) (正如 linear functional 可以被一个 covector 描述, bilinear functional 可以被一个 matrix 描述).

  • 机器学习里 training data, kernel, feature map 等都用 tensor 来描述, Python 自带的 list 和 np.array(), 统统都要转化为 torch.tensor 来进行计算 (因为 Tensor 类提供了很多现成的方法可以调用).

    import torch
import numpy as np
# python list to tensor
data_list = [[1, 2, 3], [4, 5, 6]]
list2tensor = torch.tensor(data_list)
# numpy array to tensor
data_array = np.array([[1, 2, 3], [4, 5, 6]])
array2tensor = torch.from_numpy(data_array)

Tensor Format

  • 2D tensor: (就是矩阵)
    • Row, Col (R, C): 两个维度.
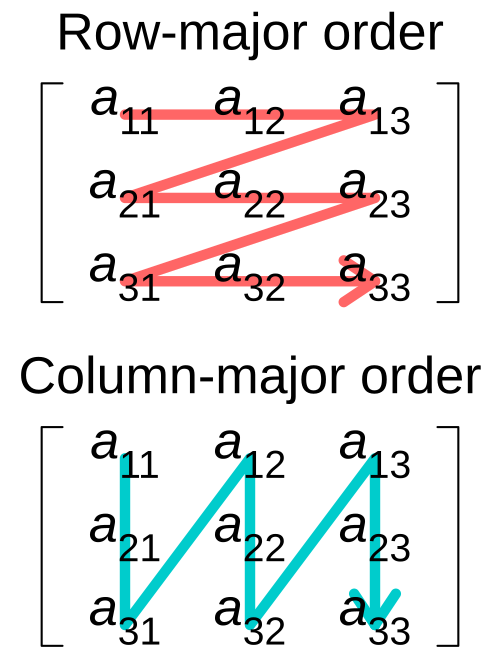
    • Memory Layout: 见 Figure fig-tensor2d-layout.
      • Row-major (RC): 先沿着行方向将数据拉直, numpy 采用.
      • Column-major (CR): 先沿着列方向将数据拉直, Eigen 采用.
Figure 1

  • 4D tensor: 特别是在图像处理中, 4D 张量非常常见, 现在单独详细研究一下它:

    • H, W, C(D), N(B) 维度语义: Height, Width, Channel(Depth), Batch size (见 Figure fig-tensor-layout 左图).

    • Memory Layout1: (注意无论多少维度的张量, 在内存中显然都是以 (也只能以) 一维数组的形式连续存储).

      • HWCN: Batch 在最后.
      • NHWC: Batch 在最前, numpy 采用.
      • NCHW: Batch 在最前, pytorch 采用 (个人感觉这是最符合直觉的顺序!)
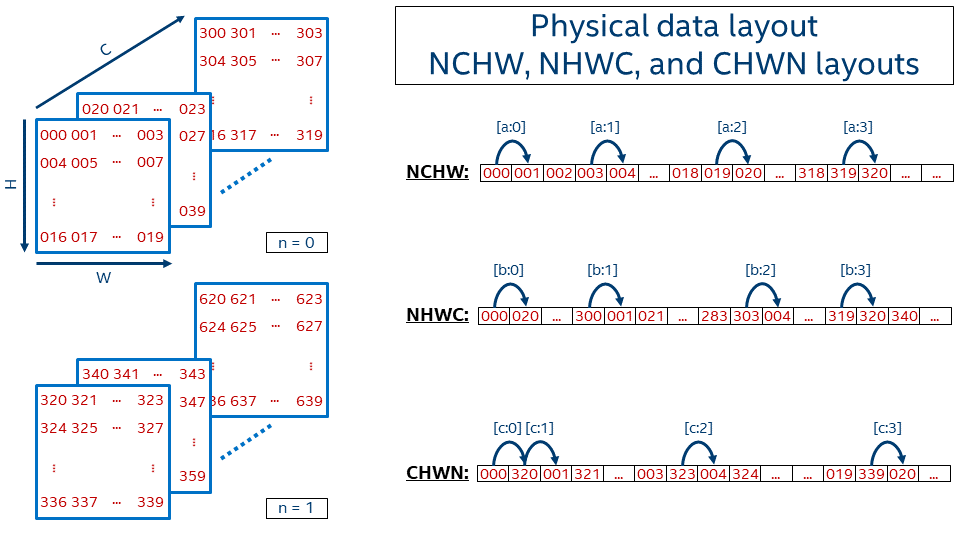
      Figure 2: 三种 Data Layout Formats [1].

1 记忆方法: 反过来看, 如 NHWC, 先沿着 C 方向将数据拉直, 结束后跳到下一个 W, 然后换 H, 最后换 N.

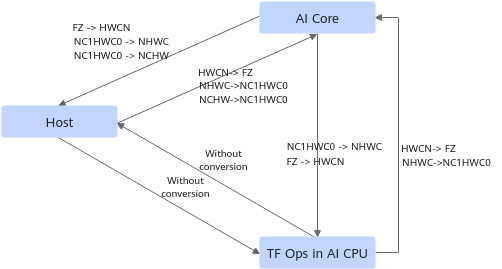
Figure 3: 不同的算子在不同的模块执行可能涉及算子的 format 转换 [2]. C0, C1 由 C 拆分得来, FZ 是另一种 tensor format.

Mental Picture of Tensors

  • 同一个中括号内用逗号分割的元素一般被认为地位相同. 比如下面 1, 2, 3 地位相同, [1,2,3] 和 [4,5,6] 地位相同.

  • Tensor size: 笔者习惯从最内层中括号开始读起, 每层中括号相同地位的元素个数即为该维度的大小, 从右向左 列出来即为 tensor shape.

    • 比如:

      torch.Size([2, 4])

      应解读为两个 [....] 而不是 4 个 [..].

    • 这里留两个练习, 给出下面两个 tensor 的 shape:

      t = torch.tensor([
    [ [1], [2],  [3],  [4]  ],
    [ [5], [6],  [7],  [8]  ],
    [ [9], [10], [11], [12] ]
])
u = torch.tensor([
    [ [ [ [1] ] ], [ [ [2] ] ] ]
])

print(t.shape)  # 输出: torch.Size([3, 4, 1])
print(u.shape)  # 输出: torch.Size([1, 2, 1, 1, 1])

  • 当我们说一个「维度」时我们在谈论什么?

    • 每个维度看到的「元素」都是「片面」且「抽象」的. 比如下面的 4 这个维度看见的画面仅仅是蓝色的「切片」, 而且它无法分清三个蓝色条条的区别.

    • 后文很多算子都有 dim 这个参数, 说明这个算子作用在这个「维度」上. 对维度 4 来说, 就是同时作用在所有的蓝色切片上!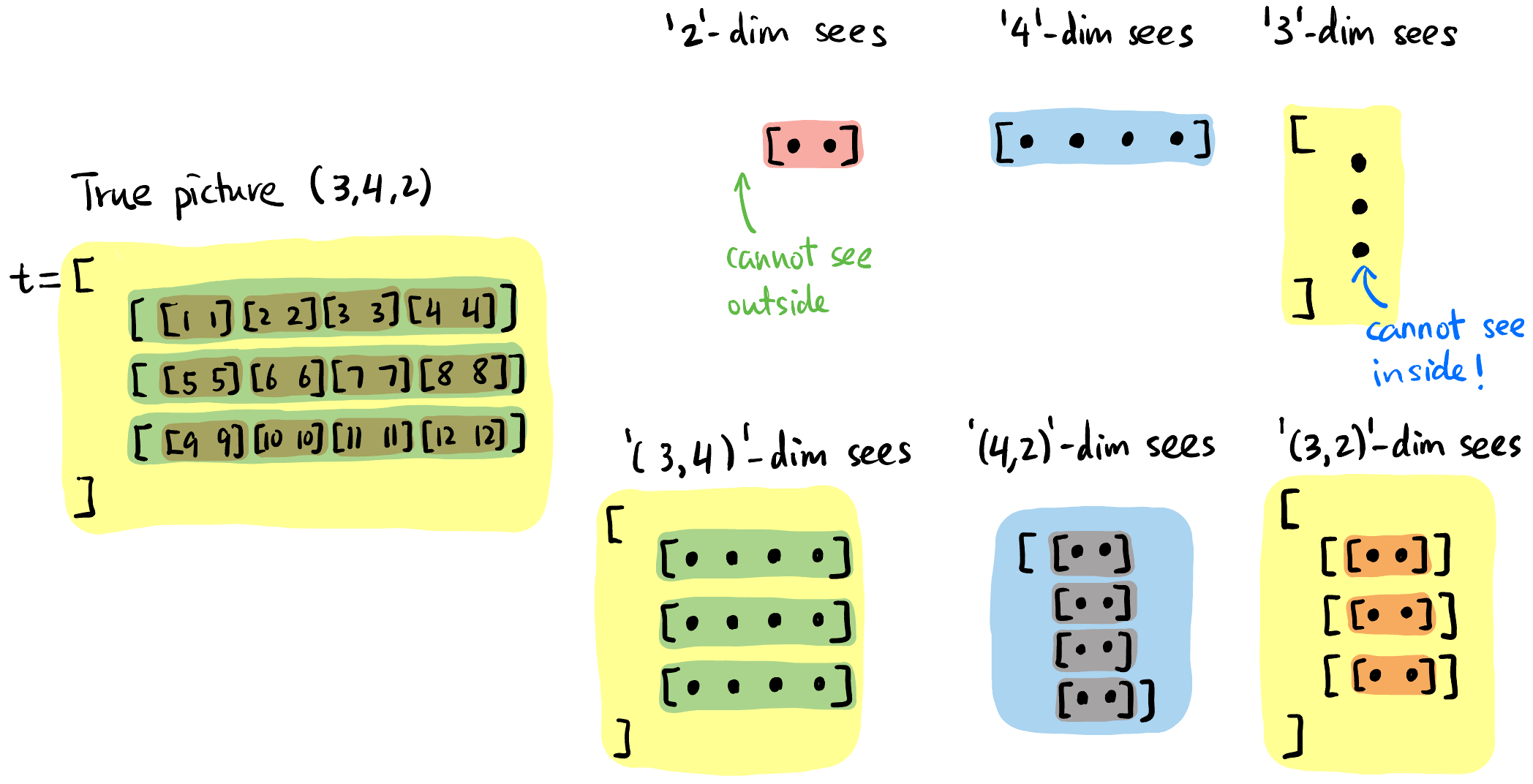

      Figure 4: 每个维度即不能看到其元素内部 (「抽象」), 也无法看到外部 (「片面」).

Tensor Operations

Tensor 形状改变 (einops 库)

einops 提供了方便的 API 来改变 tensor 的形状.

  • 所有 Tensor 形状变化构成群, 可由下面三个生成元 (Grouping, Transposition, Concatenation) 生成:

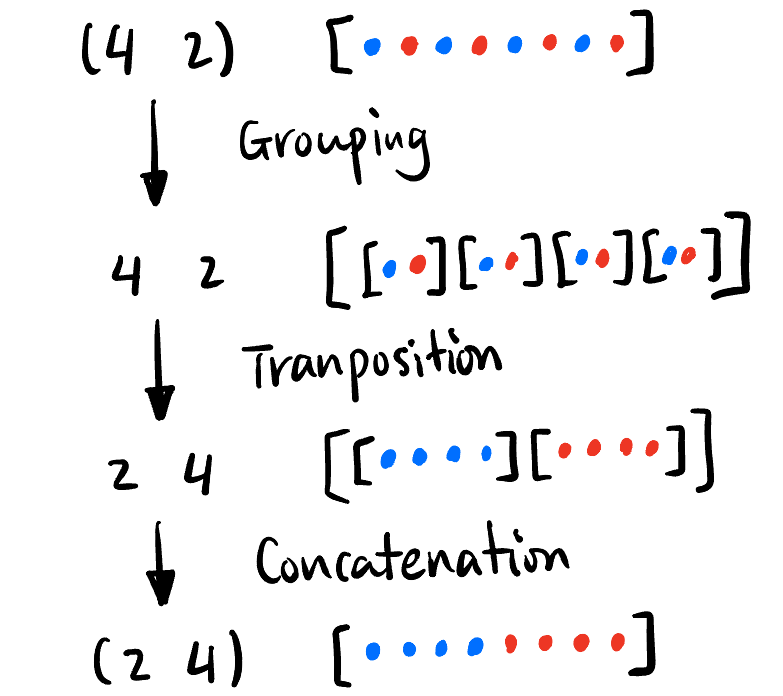
    Figure 5: Tensor 变形的三个生成元. 
    import torch
from einops import rearrange

t = torch.tensor([1,2,3,4,5,6,7,8])
t = rearrange(t, '(b a) -> b a', a=2)   # Grouping, t.shape = [4,2], t = [[1,2],[3,4],[5,6],[7,8]]
t = rearrange(t, 'b a -> a b')          # Transposition, t.shape = [2,4], t = [[1,3,5,7],[2,4,6,8]]
t = rearrage(t, 'b a -> (b a)', a=4)    # Concatenation, t.shape = [8], t = [1,3,5,7,2,4,6,8]

    • Transposition 操作也可以用:

      t.transpose(-1, -2)     # 将 t 的最后两个维度交换

      如果 t 是 torch.Size([3, 4, 1]), 则变成 torch.Size([3, 1, 4]).

  • 小练习: 给出下面 t 的操作过程和结果:

    import torch
from einops import rearrange
t = torch.tensor([
    [ [1], [2],  [3],  [4]  ],
    [ [5], [6],  [7],  [8]  ],
    [ [9], [10], [11], [12] ]
])
t = rearrange(t, 'a (b1 b2) c -> (a c) (b2 b1)', b1=2)
print(t.shape)  # torch.Size([3, 4])
print(t) # tensor([[ 1,  3,  2,  4],
                 # [ 5,  7,  6,  8],
                 # [ 9, 11, 10, 12]])

    这里的变形可以拆成:

    'a (b1 b2) c -> a (b2 b1) c -> a c (b2 b1) -> (a c) (b2 b1)'

Tensor 切分

  • chunk() 将一个 tensor 且成相等大小的多个 tensor.

    • 下面代码 chunk(num, dim) 代表将维度 dim 的「切片」分成 num 份.

      import torch
t = torch.tensor([
    [ 1,1,4,4 ],
    [ 2,2,5,5 ],
    [ 3,3,6,6 ]
])     # torch.Size([3, 4])

a, b = t.chunk(2, dim=1)
# a = tensor([[1., 1.],
#             [2., 2.],
#             [3., 3.]])
# b = tensor([[4., 4.],
#             [5., 5.],
#             [6., 6.]])

Tensor 乘加

  • Tensor 的基础运算包括:

    • Element-wise multiplication: +, -, *, / 都是逐点的.
    • Matrix-like multiplication: @ (等价于 torch.matmul() 函数).

      • 注意当对高维张量进行矩阵乘法的时候, 只要求最后两个维度满足矩阵相乘的规定 (比如 ) 即可, 前面的维度一般要求相同好进行两两配对 (见 Figure fig-tensor-matmul).

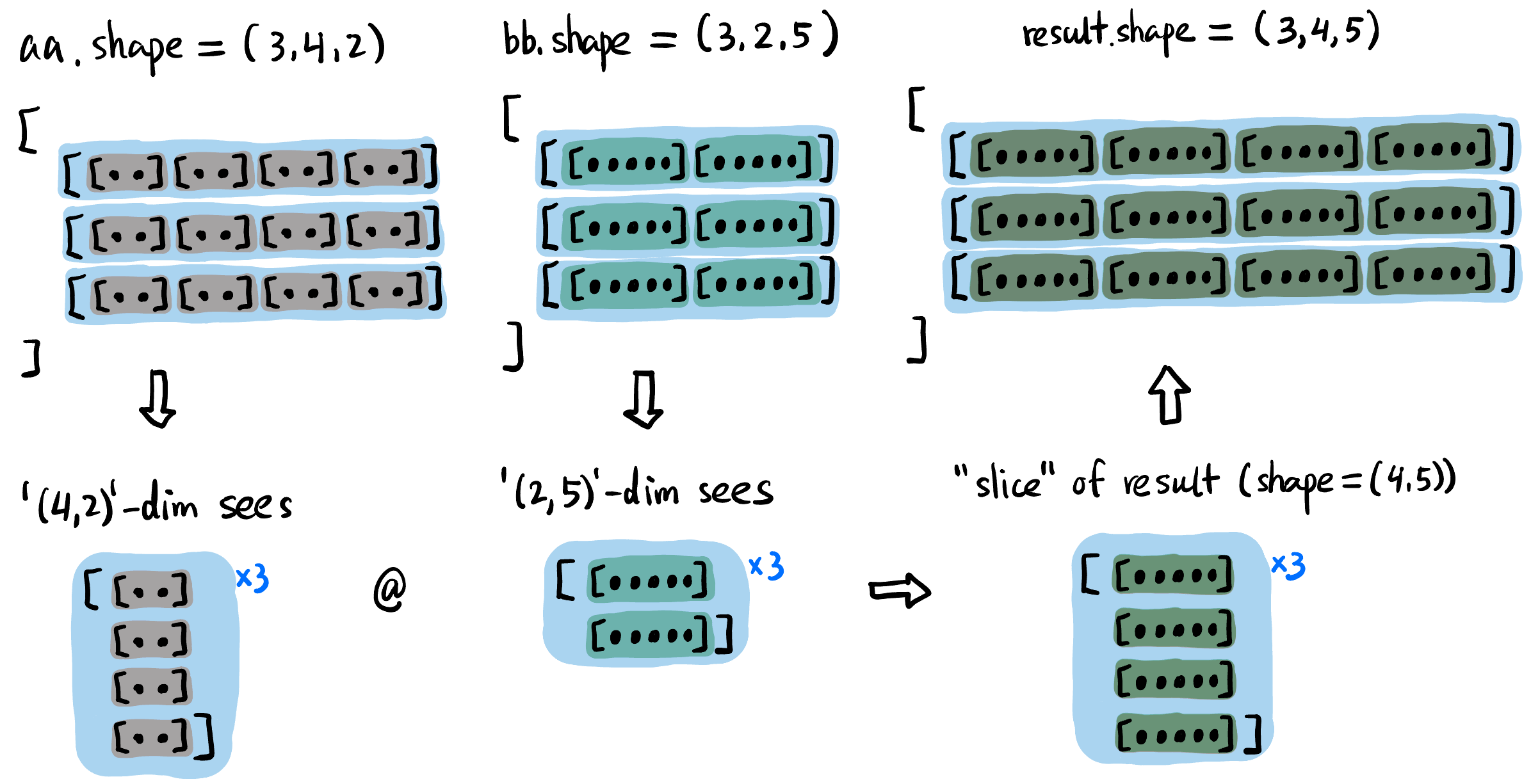
        Figure 6: aa 和 bb 矩阵乘法得到 result 的过程, 前面的维度 (3) 要求相同.

      • 思考张量矩阵乘法时将最后两维度的一个「切片」想象出来即可, 前面的维度只是这个过程的结构化重复

        • 比如 Figure fig-tensor-matmul 中只需要将右下角的「切片」按照前面的维度 3 的结构放好就行, 这里很简单直接拼接即可; 如果 aa 和 bb 前面的维度不是 3 而是复杂点的比如 (2,4,1), 思考方式没有任何变化.

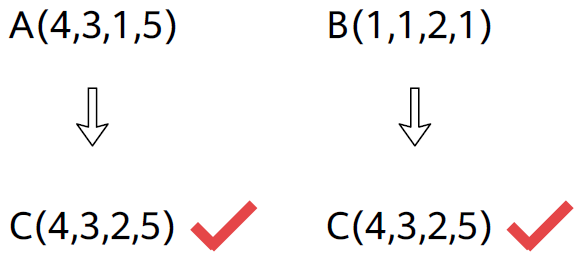
  • Tensor Broadcasting: 上面两种运算都支持 broadcasting, 指 左侧缺少的维度 或者 不匹配的相应维度是 1 的维度都会自动复制成与另一个张量一样的:

    import torch
aa = torch.randn(2,3,6,5,4)     # base tensor

bb = torch.randn(  3,6,5,4)
cc = torch.randn(2,3,6,5  )
dd = torch.randn(2,3,  5,4)
ee = torch.randn(2,3,1,5,4)
ff = torch.randn(2,3,2,5,4)

## Element-wise operation (+ - * / 都是逐点的)
add1_ew = aa + bb        # 可以自动填充左侧维度, add1_ew 大小 [2,3,6,5,4]
# add2_ew = aa + cc      # 不能自动填充右侧维度!
# add3_ew = aa + dd      # 不能自动填充中间维度!
add4_ew = aa + ee        # 1 维度自动复制 6 份, add4_ew 大小 [2,3,6,5,4]
# add4_ew = aa + ff      # 中间的 2 维度不能自动复制 3 份! (虽然理论上是可以定义的)

gg = torch.randn(2,3,6,4,5)
hh = torch.randn(2,3,6,1,5)

## Matrix multiplication (@ 与 torch.matmul() 函数效果一样)
matmul1 = aa @ gg        # 最后两个维度满足矩阵相乘要求就行, matmul1 大小 [2,3,6,5,5]
matmul2 = aa @ bb.transpose(-1,-2)      # 可以自动填充左侧维度, matmul2 大小 [2,3,6,5,5]
# matmul3 = aa @ dd.transpose(-1,-2)    # 不能自动填充中间维度!
matmul4 = aa @ ee.transpose(-1,-2)      # 1 维度自动复制 6 份, matmul4 大小 [2,3,6,5,5]
# matmul5 = aa @ ff.transpose(-1,-2)    # 中间的 2 维度不能自动复制 3 份! (虽然理论上是可以定义的)
# matmul6 = aa @ hh                     # 最后两个维度必须严格满足矩阵相乘规定, 没有 broadcasting 的说法.
Figure 7: 逐点运算之前要进行 tensor broadcasting.

神经网络的常见层

下面我们列举一些神经网络中的一些层, 它们仅仅是对 tensor 的一些操作.

带参数的层

  • Convolution 卷积层: 匹配 NCHW 中的 C.

    t = torch.randn(2,3,5,4)
t1 = nn.Conv2d(in_channels=3, out_channels=6, kernel_size=3, padding=1)(t)

  • Linear 线性层: 匹配最右边的维度.

    t = torch.randn(2,10)
t1 = nn.Linear(in_features=10, out_features=5)(t)

无参数的层

  • 「切片」操作: 对 tensor 某一维度的处理.

    • Softmax: 下面代码 Softmax(dim=1) 表示在 t 的第 2 个维度「切片」的整体做 softmax.

      t = torch.tensor([
    [ 1,1,1,1 ],
    [ 2,2,2,2 ],
    [ 3,3,3,3 ]
], dtype=torch.float32)     # torch.Size([3, 4])
t = nn.Softmax(dim=1)(t)    # tensor([[0.2500, 0.2500, 0.2500, 0.2500],
                                    # [0.2500, 0.2500, 0.2500, 0.2500],
                                    # [0.2500, 0.2500, 0.2500, 0.2500]])
  • 其它操作
    • 激活函数: SiLU()
    • 恒等映射: Identity()
    • Dropout: 训练时随机置 0, 推理时自动关闭.
    • 下采样: AvgPool2d()

Autograd 机制

Motivation

  • 如何在计算机中进行微分?

    • Manual Differentiation: 人工推导导数公式, 然后写进代码.

    • Symbolic Differentiation: 计算机符号化地推导导数公式, 然后生成代码 (Mathematica 就是这么干的)

    • Numerical Differentiation: 用数值方法近似地计算导数.

    • Automatic Differentiation: 通过链式法则和计算图, 自动地计算导数.

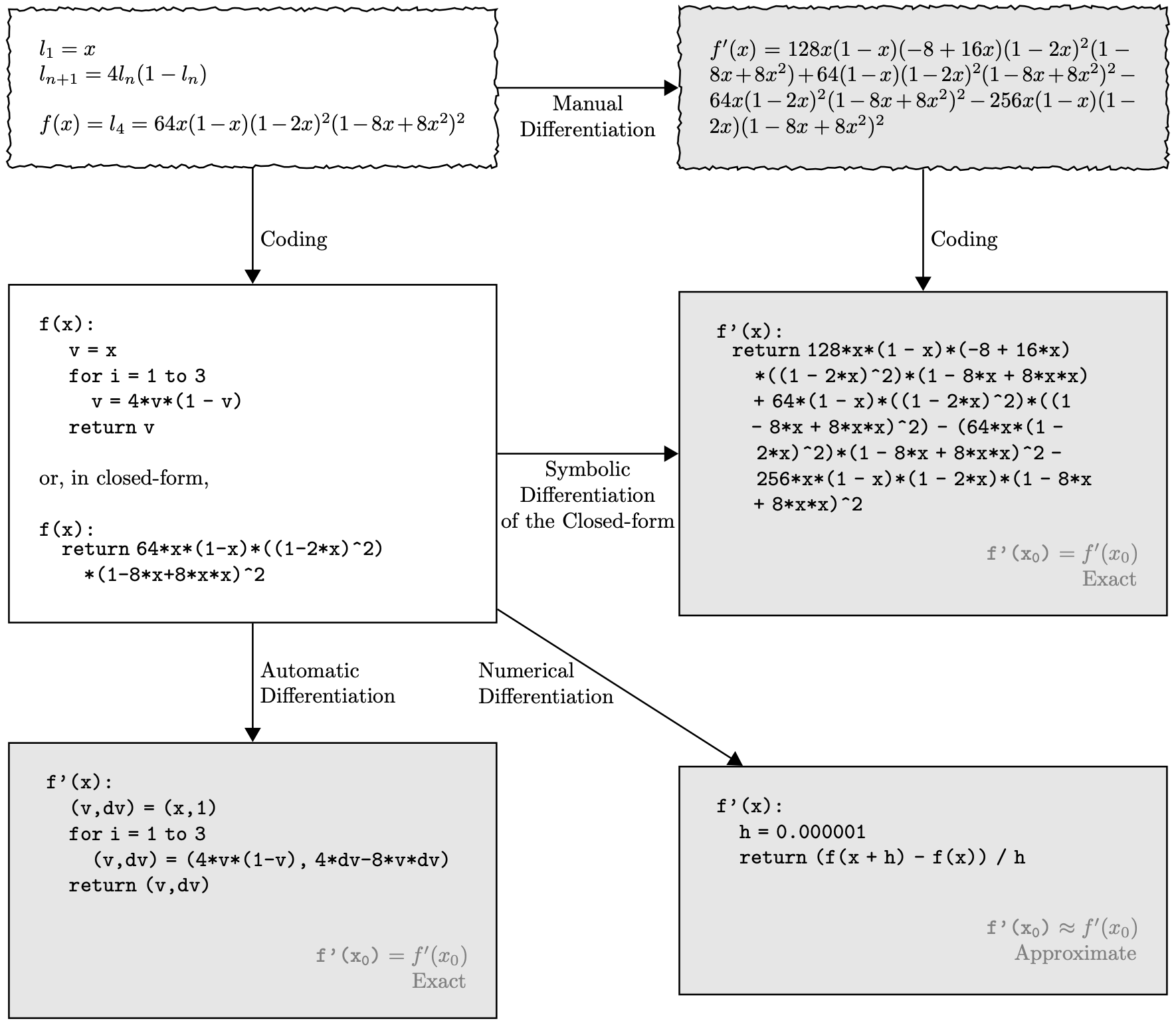
      Figure 8: 计算机中微分的 4 种方式 [3].
  • 放在 ML 的场景下, 一个神经网络可能有几十亿的参数, 每个参数都要求梯度, 手动推导不可能完成! 符号化推导也会导致表达式爆炸, 数值方法精度又不够好. 但是神经网络的函数不是随意的函数, 它是高度算子化和分层的. 我们希望导数的信息能自动沿着计算的路径 (Computational Graph) 反向传播!
    • 用「传播」这个词是因为神经网络是高度分层的结构, 数据之间有明显的依赖关系 (partially-ordered).
    • 用「自动」这个词是因为我们希望一句 loss.backward() 就能像遍历一个树一样完成所有的梯度计算.
    • 而且我们希望在程序看来每个梯度计算都是「局部」的, 运行的函数并不知道自己在传播一个大计算图.
      • 这个理论基础是 Chain Rule 链式法则! 我们这样解读链式法则: 要求 \(y\) 关于变量 \(v\) 的导数, 只要知道下面三类信息 (在 Figure fig-chain-rule 标为蓝色):
        • \(v\) 参与了哪些算子的运算;
        • 这些算子的输出 (当然每个算子只有一个) 分别对 \(y\) 的导数;
        • 这些算子的其它输入的值.
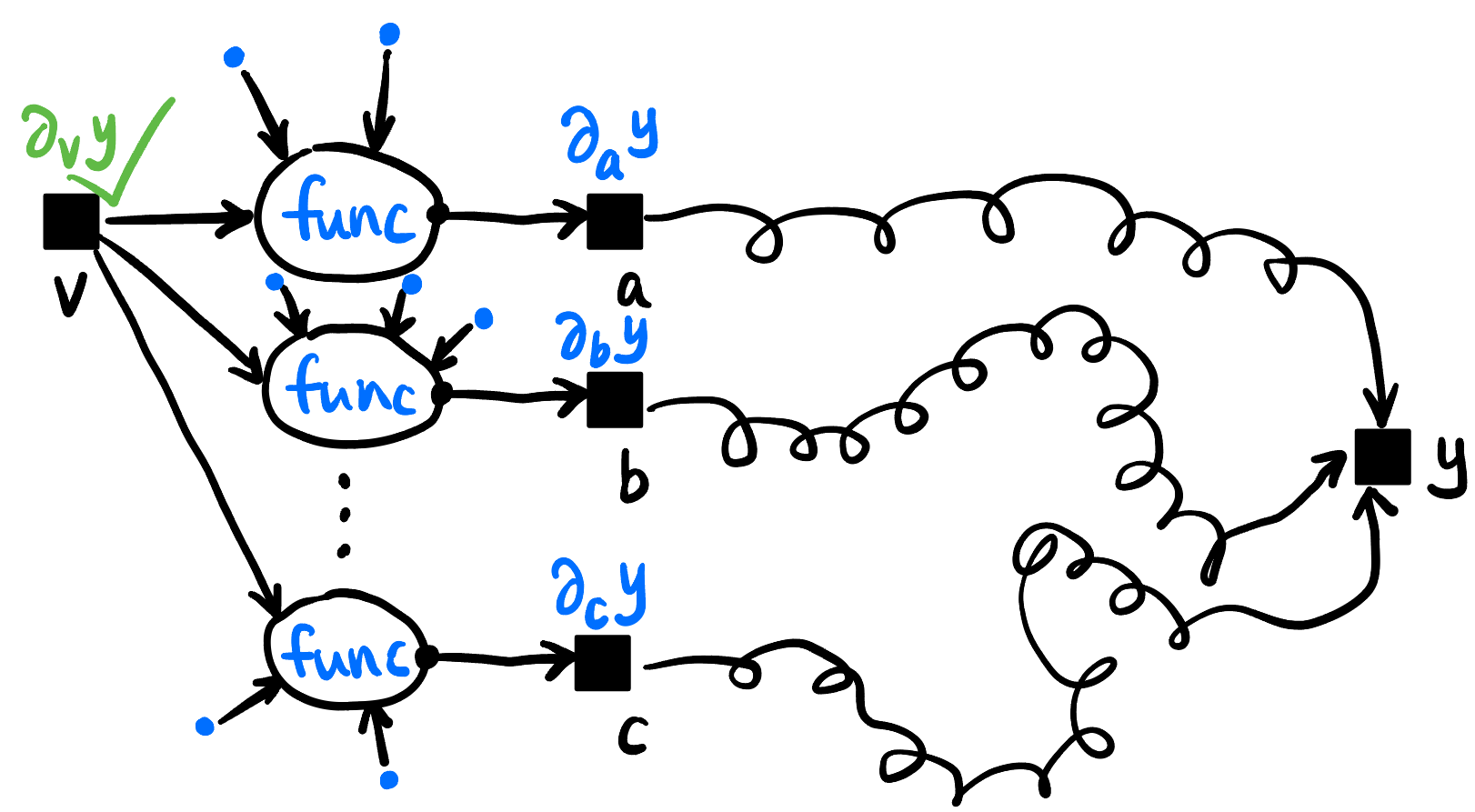
        Figure 9: Chain Rule 的局部视角, 求 \(\partial_v y\) 只需要知道蓝色的信息, 对于 \(a,b, \ldots, c\) 与 \(y\) 的关系不需要知道!
EXAMPLE: A scalar computational graph

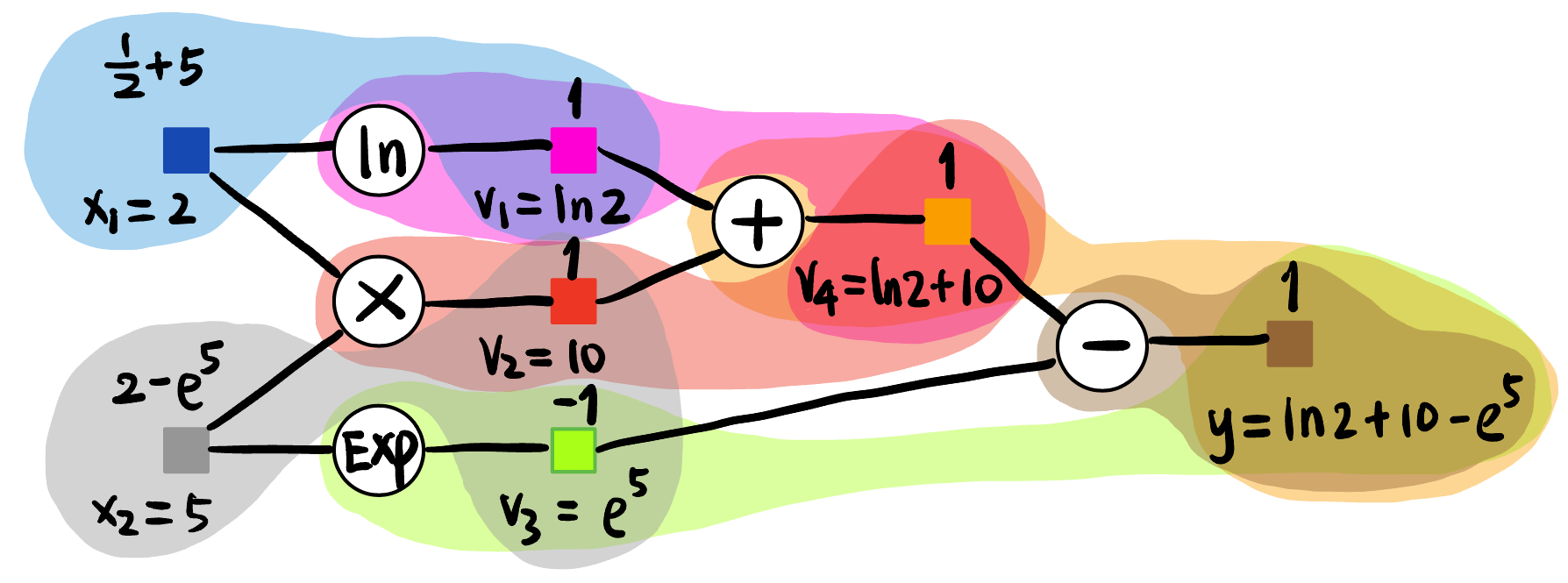
考虑式子 [4]: \[ y := \ln x_1 + x_1 x_2 - e^{x_2} \tag{1}\]

可以由以下图表示:

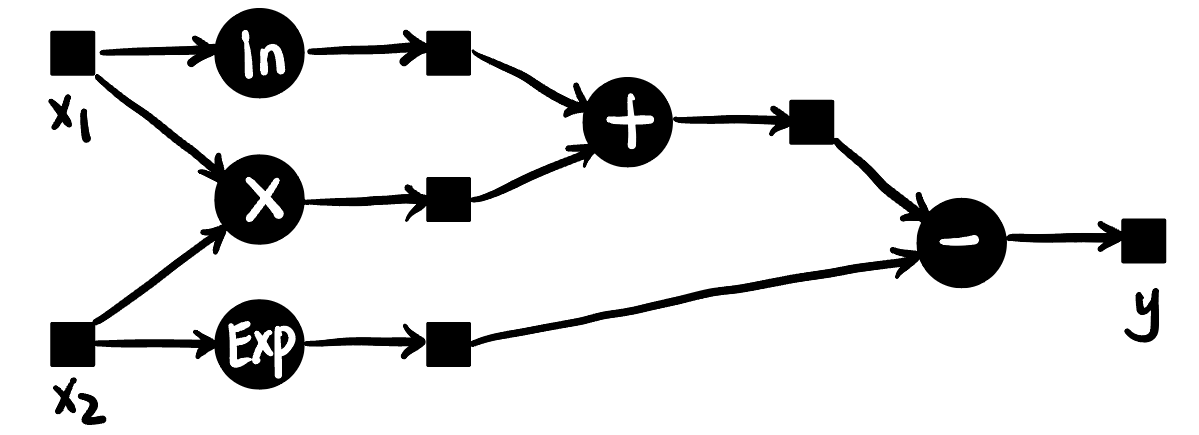
Figure 10: Computational graph demo.

我们希望计算 \(y\) 关于 \(x_1, x_2\) 在 \((x_1, x_2) = (2, 5)\) 处的梯度.

  • Forward propagation: 首先进行前向传播, 目的是计算出中间变量的数值 (为什么要算呢, 因为链式法则需要知道中间变量的值!):

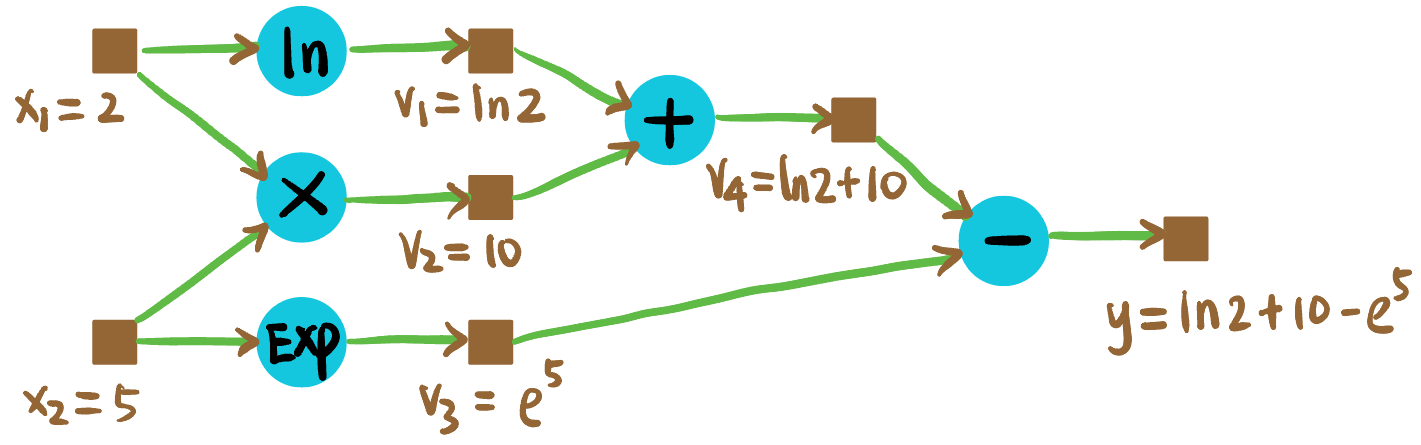
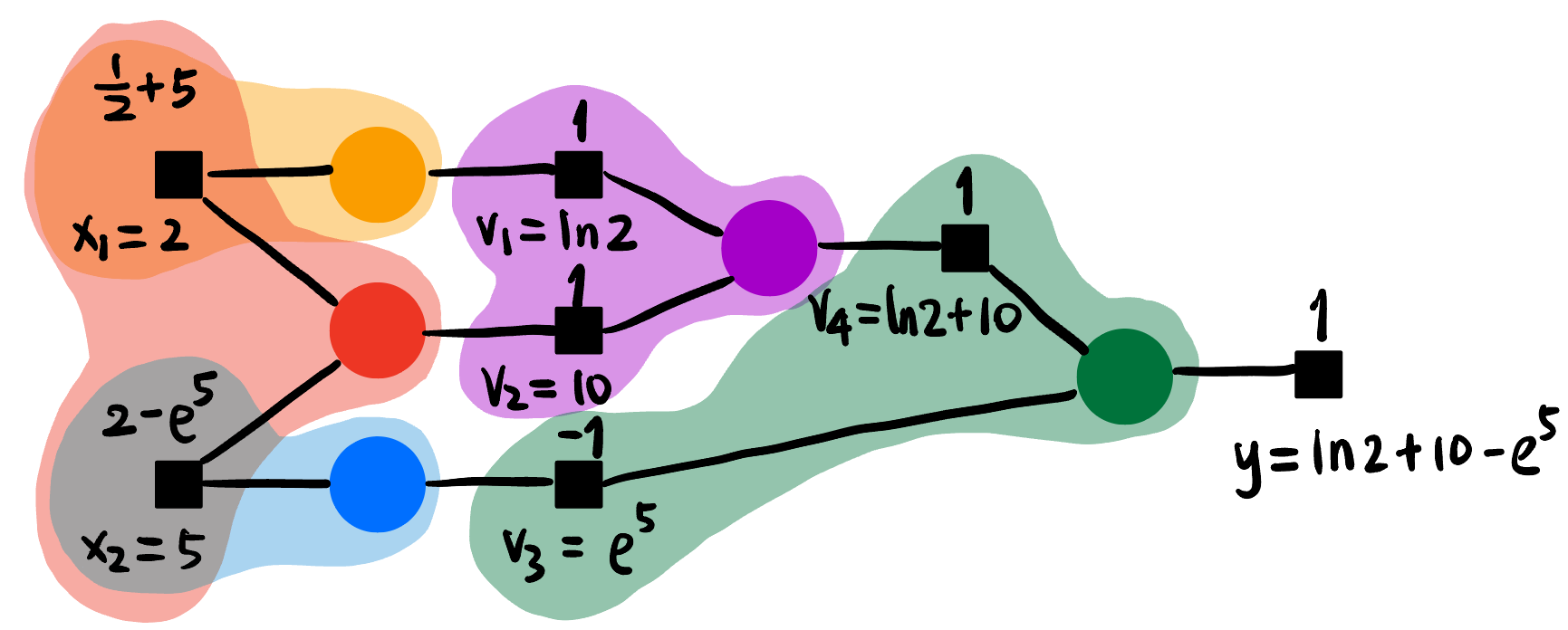
    Figure 11: Forward propagation.

  • Backward propagation: 如 Figure fig-ex-backward, 蓝色数值代表 \(y\) 对该节点的导数.

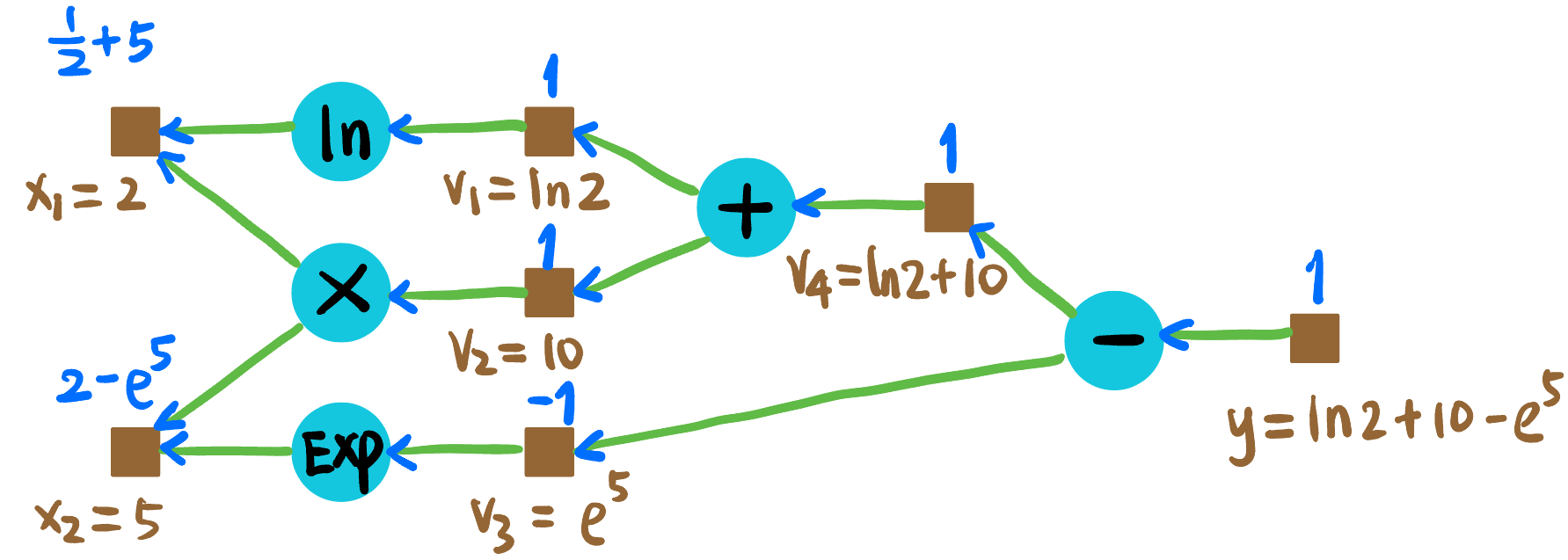
    Figure 12: Backward propagation.

可知:

\[ \begin{aligned} \partial_{x_1} y &= 5.5 \\ \partial_{x_2} y &= -146.4 \end{aligned} \]

Minimal Implementation

我们将 Figure fig-ex-forward 的棕色方块建模为 Tensor 类, 青色圆形建模为算子比如 Add. 这是 autograd 重点关注的两个结构. 现在我们实现 Equation eq-example 的 autograd 库 (只实现了必要的算子, adapted from [5]). 主要关注 Tensor 类的 backward() 方法和各个算子的 backward() 方法的相互调用!

mytorch/tensor.py
from __future__ import annotations
from typing import Optional
import numpy as np

class Tensor:
    def __init__(self, data: np.ndarray, requires_grad=False, operation=None):
        # Payload
        self.data = data
        # Metadata
        self.requires_grad = requires_grad
        if self.requires_grad:
            self.grad = np.zeros_like(data, dtype=np.float32)
        self.operation = operation  # What operation cls created this tensor
        self.children = []          # What other tensors are created from this tensor

    # This method is called by the operation backward()
    def backward(self, 
                 grad_: Optional[np.ndarray] = None,    # The downstream operator pass this gradient for you
                 z: Optional[Tensor] = None):           # Which child tensor is passing the gradient
        if not self.requires_grad:
            return "Cannot backpropagate on a tensor that does not require gradients."
        
        if grad_ is None:           # Called only the first time from loss.backward()
            grad_ = np.ones_like(self.data, dtype=np.float32)   # Set a tiny nudge of ones
            
        self.grad += grad_          # Aggregate gradients from that children (but possibly not all yet)
        
        if z is not None:           # NOT called only the first time
            self.children.remove(z) # I heard the gradient from you, no need to wait for you anymore
        
        if self.operation:
            if not self.children:   # Received grad_ from all children, ready to pass grad upstream
                self.operation.backward(self.grad, self)
            
    # Some basic operators, more operators must be called via their classes below
    def __add__(self, other: Tensor) -> Tensor:
        op = Add()
        return op.forward(self, other)

    def __neg__(self) -> Tensor:
        op = Neg()
        return op.forward(self)

    def __sub__(self, other: Tensor) -> Tensor:
        return self + (-other)
    
    def __mul__(self, other: Tensor) -> Tensor:
        op = Mul()
        return op.forward(self, other)
    

# These are just operators
class Add:
    def forward(self, a: Tensor, b: Tensor) -> Tensor:
        # Record which two tensors were added
        self.parents = (a, b)
        
        # Create result tensor z
        requires_grad = a.requires_grad or b.requires_grad
        data = a.data + b.data
        z = Tensor(data, requires_grad=requires_grad, operation=self) 
        
        # Side effects to a, b
        a.children.append(z)
        b.children.append(z)

        return z
        
    def backward(self, dz: np.ndarray, z: Tensor):
        a, b = self.parents
        
        if a.requires_grad:
            da_ = dz
            a.backward(da_, z)
        if b.requires_grad:
            db_ = dz
            b.backward(db_, z)

class Neg:
    def forward(self, a: Tensor) -> Tensor:
        # Record which tensor was negated
        self.parent = a
        
        # Create result tensor z
        requires_grad = a.requires_grad
        data = -a.data
        z = Tensor(data, requires_grad=requires_grad, operation=self) 
        
        # Side effects to a
        a.children.append(z)

        return z
        
    def backward(self, dz: np.ndarray, z: Tensor):
        a = self.parent
        
        if a.requires_grad:
            da_ = -dz
            a.backward(da_, z)

class Mul:
    def forward(self, a: Tensor, b: Tensor) -> Tensor:
        # Record which two tensors were multiplied
        self.parents = (a, b)
        
        # Create result tensor z
        requires_grad = a.requires_grad or b.requires_grad
        data = a.data * b.data
        z = Tensor(data, requires_grad=requires_grad, operation=self) 
        
        # Side effects to a, b
        a.children.append(z)
        b.children.append(z)

        return z
        
    def backward(self, dz: np.ndarray, z: Tensor):
        a, b = self.parents
        
        if a.requires_grad:
            da_ = dz * b.data
            a.backward(da_, z)
        if b.requires_grad:
            db_ = dz * a.data
            b.backward(db_, z)
            
class Exp:
    def forward(self, a: Tensor) -> Tensor:
        # Record which tensor was exponentiated
        self.parent = a
        
        # Create result tensor z
        requires_grad = a.requires_grad
        data = np.exp(a.data)
        z = Tensor(data, requires_grad=requires_grad, operation=self) 
        
        # Side effects to a
        a.children.append(z)

        return z
        
    def backward(self, dz: np.ndarray, z: Tensor):
        a = self.parent
        
        if a.requires_grad:
            da_ = dz * z.data   # since d(exp(a))/da = exp(a)
            a.backward(da_, z)
            
class Log:
    def forward(self, a: Tensor) -> Tensor:
        # Record which tensor was logged
        self.parent = a
        
        # Create result tensor z
        requires_grad = a.requires_grad
        data = np.log(a.data)
        z = Tensor(data, requires_grad=requires_grad, operation=self) 
        
        # Side effects to a
        a.children.append(z)

        return z
        
    def backward(self, dz: np.ndarray, z: Tensor):
        a = self.parent
        
        if a.requires_grad:
            da_ = dz / a.data   # since d(log(a))/da = 1/a
            a.backward(da_, z)

写一个测试程序:

tensor-backward.py
import mytorch as torch
import numpy as np

x1 = torch.Tensor(np.array([2]), requires_grad=True)
x2 = torch.Tensor(np.array([5]), requires_grad=True)

v1 = torch.Log().forward(x1)
v2 = x1 * x2
v3 = torch.Exp().forward(x2)

v4 = v1 + v2

loss = v4 - v3
print("loss =", loss.data)

loss.backward()

print("x1.grad =", x1.grad)
print("x2.grad =", x2.grad)

运行结果:

loss = [-137.72001192]
x1.grad = [5.5]
x2.grad = [-146.41316]
Figure 13: 每个 tensor 包含 data, grad (y 对它的导数), 创建它的 operator 和依赖它的 tensors (红色的 tensor 含有红色区域的信息, etc.)
Figure 14: 每个 operator 包含它所有的 operands (红色的算子含有红色区域的信息, etc.)

References

[1]
“Understanding memory formats.” Intel, 2023. Available: https://www.intel.com/content/www/us/en/docs/onednn/developer-guide-reference/2023-1/understanding-memory-formats.html. [Accessed: Jan. 03, 2026]
[2]
Ascend Community, “Operator basics.” Hiascend.com, Sep. 2025. Available: https://www.hiascend.com/document/detail/en/canncommercial/800/opdevg/tbeaicpudevg/atlasopdev_10_0006.html. [Accessed: Feb. 09, 2026]
[3]
A. G. Baydin, B. A. Pearlmutter, A. A. Radul, and J. M. Siskind, “Automatic differentiation in machine learning: A survey.” 2018. Available: https://arxiv.org/abs/1502.05767
[4]
deep_thoughts, “Derive autograd forward and reverse propagation from scratch.” Bilibili.com, Nov. 2021. Available: https://www.bilibili.com/video/BV1PF411h7Ew?spm_id_from=333.788.videopod.sections&vd_source=42579e22289b6144ba0b2bdcf99834e3. [Accessed: Feb. 02, 2026]
[5]
E. Leitão, “Documented and unit tested educational deep learning framework with autograd from scratch.” GitHub, Mar. 2024. Available: https://github.com/eduardoleao052/Autograd-from-scratch. [Accessed: Feb. 02, 2026]