Algorithm Notes 算法笔记

C3 算法

C3 线性化算法是 Python 用来确定类继承顺序 (MRO, Method Resolution Order) 的算法.

Motivation: 具有多重继承的 一些 class 可以抽象为一个 poset 偏序集, 我们需要设计一种方法将其拉直, 这样当一个子类没有某方法时可以按照某种确定的顺序去父类中寻找该方法!
- 稍微严谨一点来说: 对于一个 poset, 任意挑选一个节点 \(A\), 我们需要定义一个方法 \(L\), 它返回唯一的一条以这个节点开头的 list \(L[A]=[A, \cdots]\)
- 当然我们对 \(L\) 有一些限制条件:
  - 所有的父类都应该在它的子类之前出现
  - 父类也有顺序 (由代码中继承的顺序决定), 比如下面就要求 F 在 G 前面, G 在 H 前面 (但不一定挨着, 只要出现在之前就行):
```
class I(F, G, H):
    pass
```
- 显然满足以上条件的 \(L\) 不止一种, 比如:
  
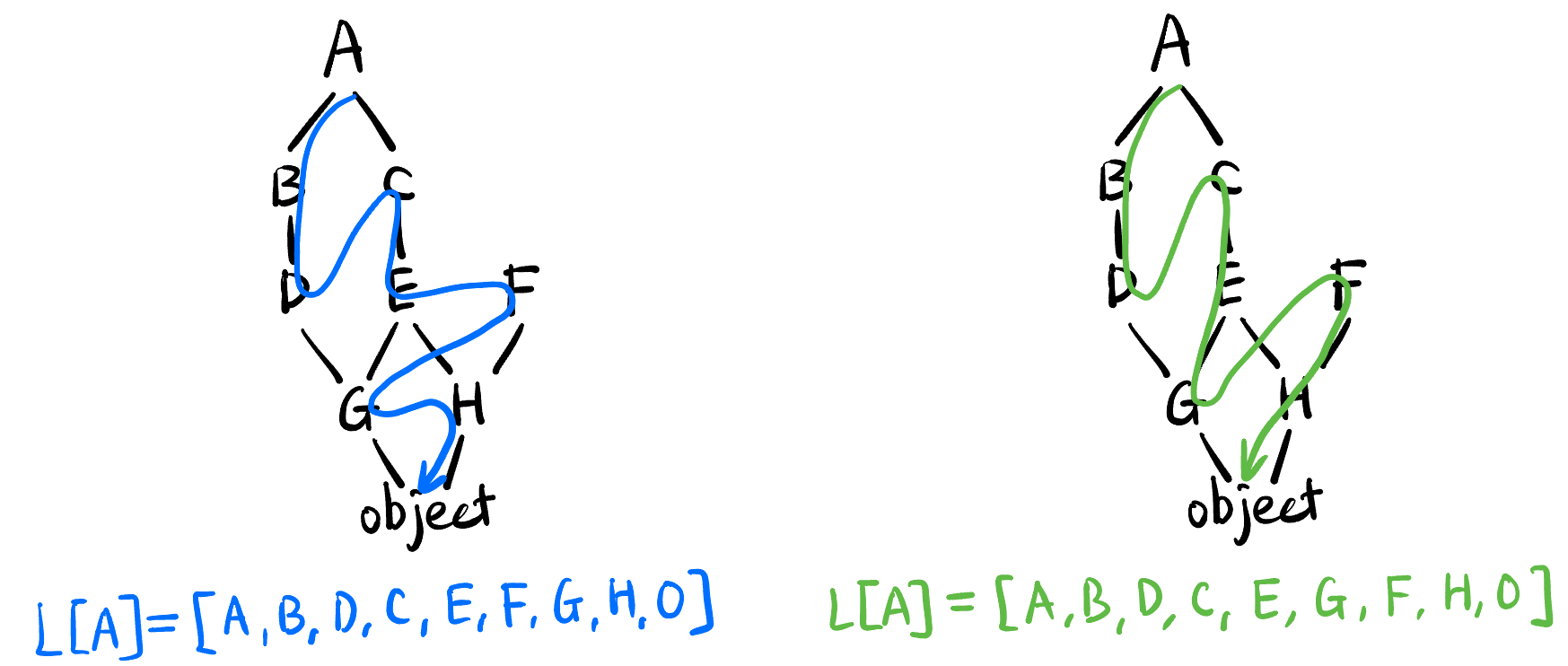
  Figure 1: 满足两条限制条件的 \(L\) 不止一种 (右图才是 C3 算法).
- Python 里可以用 print(ClassName.__mro__) 查看这个类返回的 list (称为 MRO).
C3 算法的开发者想出了一个 ad hoc 的方法 (我感觉这个定义相当随意, 我有可能错): 定义 merge() 函数, 它将不同的有序 list 合并, 合并的结果保持所有 list 的序关系!
- 每次从上往下选择 head 中第一个出现的 valid 的节点.
- valid 的定义是: 该节点不在任何其它 list 的 tail 中出现 (这一步的原因是比如 \(A\) 在 tail 中出现了, 说明 \(A\) 前面肯定还有它的父类没有被选中, 不能选 \(A\)).
- 选中后将该节点从所有 list 中删除.
- 直到所有 list 都为空为止.

EXAMPLE: C3 merge() 函数的工作过程

Figure fig-c3-demo 展示了:

\[ \text{merge}([B,A,O],[C,A,O],[D,O],[B,C,D]) = [B,C,D,A,O] \] 的计算过程.

利用 merge() 函数写出 C3 算法的递归表达式:

\[ L[\text{Node}] = [\text{Node}] + \text{merge}(L[\text{Parent}_1], \cdots, L[\text{Parent}_n], [\text{Parent}_1, \cdots, \text{Parent}_n]) \]

其中 \(\text{Parent}_1, \cdots, \text{Parent}_n\) 是类 \(\text{Node}\) 的所有父类.
- 比如对于 Figure fig-c3-candidate 中节点 \(E\):
  
  \[ L[E] = [E] + \text{merge}(L[G], L[H], [G,H]) \]
- 基于这个式子递归即可.