EDA Notes 笔记

Takeaways

  • 处处都是优化问题, 一般的思路就是先 brainstorm 你能想到的要减小的「因素1」, 然后一股脑全加起来作为 Loss function. 然后:
    • [1] 给我们的启发就是将这个问题等价变成一个训练神经网络的问题, 利用 torch 的生态来并行计算.
    • 如果 Loss function 里有不可微的部分. 两种办法:
      • 直接分段函数哈哈哈 (反正 torch 里面也是用查找表算的梯度, 它也不知道它优化的函数可不可微哈哈, 这个办法在 [2] 叫做 subgradient, 但是很多时候如果微小自变量的变化输出不变时会导致训练停滞! 如果梯度突变的话有可能带来震荡和停滞).
      • 用某种平滑的方法来强行可微, 方法很多, 你也可以自己设计.

1 要增大的话填负号即可; 当然这些「因素」很多时候是相互冲突的, 而且有些「因素」比较定性, 一时间很难想出清晰的表达式, 即使有清晰的表达式计算量也极其大.

  • Net weight [1] 的 idea 告诉我们有些难以单读开一个表达式的「因素」可以融入其它的「因素」里!

  • 体会概念背后的直觉意义而不是定义本身

    • 这在数学和工程学上同样重要. 学科中都有很多「原子」概念, 比如数学中的 group, topological space, EDA 中的 pin, node 等, 他们封装了一些非常基本的思想, 出现频率非常高, 需要牢记. 但是在科研领域, 会发现出现了很多为了研究某种特定的对象外延出来或者人为定义的新概念, 比如数学中的 Schwartz space (为了严格化 Fourier transform 而定义的函数空间), \(\pi\)-system / semialgebra (为了定义 measure 而定义的集合族), EDA 中的 net slack (为了外延 slack 到 net 上而人为定义的量2) 和 Criticality [1], 它们没有所谓的「正确」定义, 只要定义出来的量能够反映你想表达的东西即可. 不需要花时间记住定义问题, 理解作者的研究方法和解决问题的思路! 如果作者没有说明具体定义, 大不了你自己定义一个类似的量来替代它们!
    • 再比如 Netlist \((V, E)\) 的两种定义方式, “Undirected convention”, lol.

2 Slack 本来是针对某个 pin/node 定义的, [1] 却不加定义地在文章中使用了 “net slack” 这个概念, 可见作者想去度量一个 net 的时序违规程度, 如何定义呢? 可以用该 net 中所有 sink 的最坏 slack, 当然也可以用该 net 中所有 sink 的 slack 之和, 没有唯一答案!

  • Unitary operator 的思考方式: 当作没有!
    • 比如定义 \(\tilde{w} := \log w\), 由于 \(w\) 和 \(\tilde{w}\) 的单调性, 优化问题不会变, 思考的时候直接忽略 \(\log\) 就行了 [1].

Some Terms

  • Hypergraph 超图: 图的一种推广, Netlist 常被建模成 (Directed [1]) hypergraph \((V, E)\) (edge 可以有多个 vertex). 一般有 Node-level 和 Pin-level 两种定义方式:

    • \(V\):
      • 如果 \(V\) 中的元素的坐标是可以独立更新的, 则其中的元素代表 cell/macro (统称为 node [1], [2] 或 instance [3], 注意不能理解为 pin, 多个 pin 可能属于同一个 cell/macro, 他们的相对位置是固定的不能独立更新).
      • 如果不关心 \(V\) 中元素的坐标更新, 有时 \(V\) 也代表 pin 集.
    • \(E\) 有直接连接关系的 node 集合, 其中的元素称为一个 net.
      • 在 Timing-driven placement 里, 一般 \(E\) 可能仅代表 Timing arc 集合.
      • “Undirected convention”: 虽然 hypergraph 是 directed 的, 即 edge 集在数学上表现为比如: \[E = \bigl\{\{(p_1, p_3), (p_2, p_3), \cdots\}, \{(p_4, p_6), (p_5, p_6), \cdots\}, \cdots \bigr\}\] E.g., \[E \ni e = \{(p_1, p_3), (p_2, p_3), \cdots\}\] 但为了 Notation 的简洁性, 我们还是把 \(E\) 当作 vertex 的集合来看待 (即看作 undirected hypergraph): \[E \ni e = \{p_1, p_2, p_3\}\]
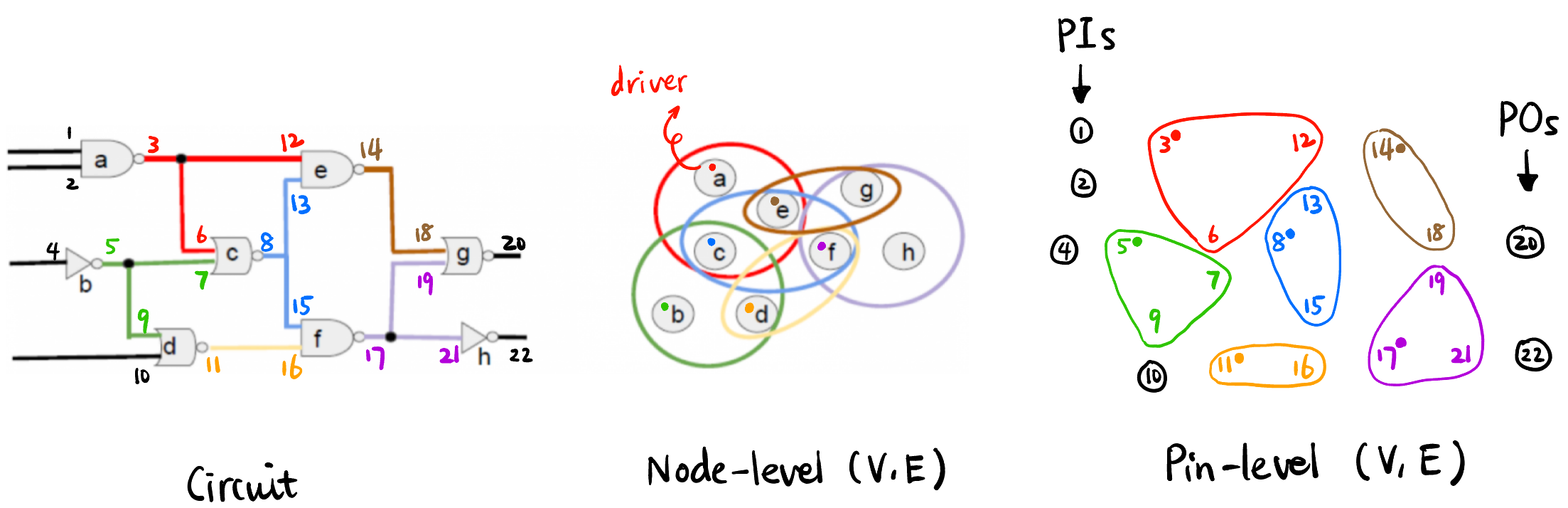
    Figure 1: Directed Hypergraph \((V, E)\) 的两种意义 (Adapted from [4], 采用 “Undirected convention”); Pin-level 的 \(E\) 之间一定没有 intersection; PIs (primary inputs); POs (primary outputs).

  • Layout: 元件或电路的 electric function 的几何图形表示 [5].

  • Standard Cell (std cell) 标准单元: 一组实现逻辑门的物理单元 (AND, OR, NOT, NAND, etc.) [5]. 他们过于基础以至于被称为 “standard”.

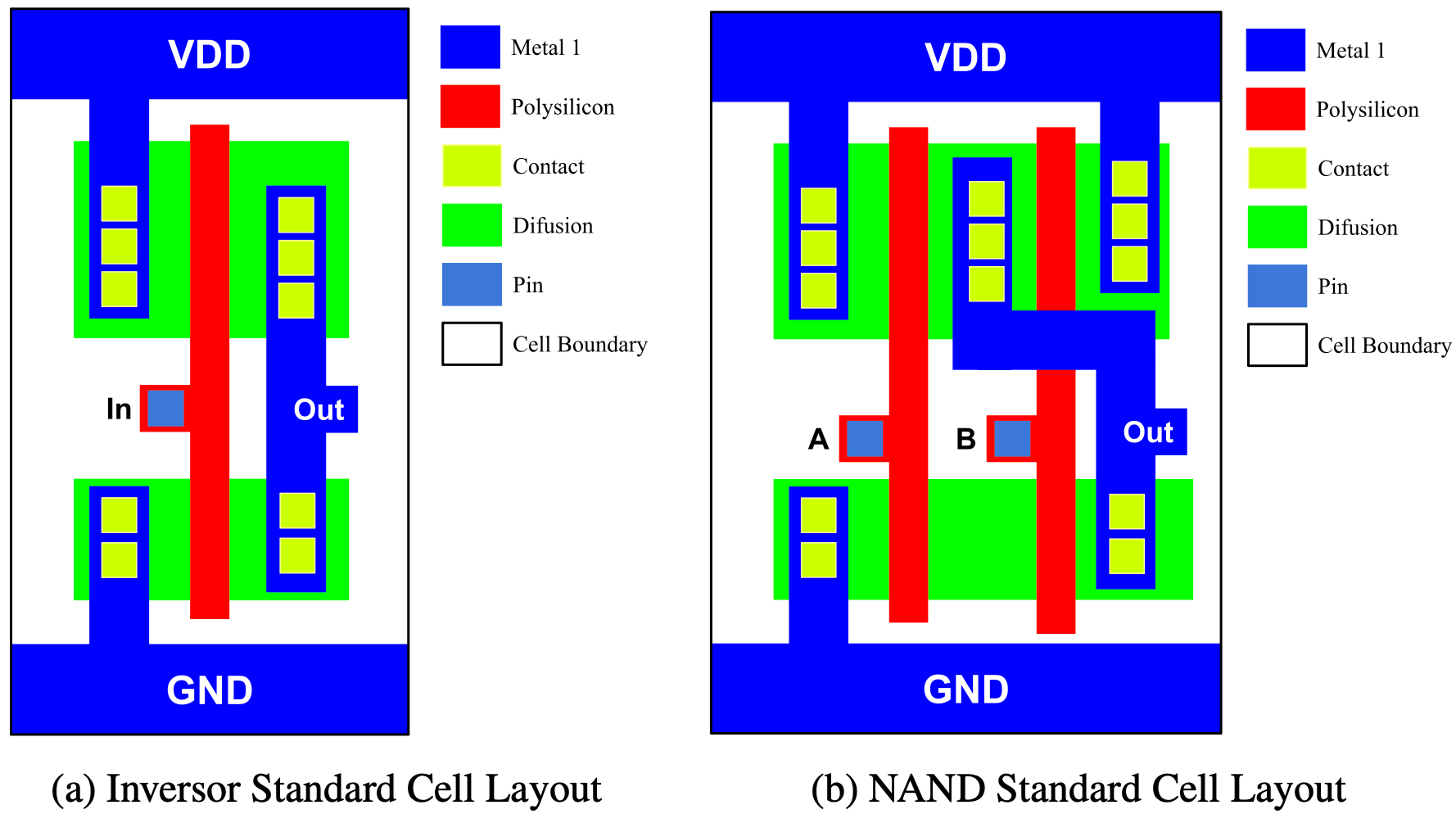
    Figure 2: NOT 和 NAND 的 layout [5]
Figure 3: Std cell height 可以是 row height 的整数倍 [5] (其实 Std cell width 也可以是 site width 的整数倍).

Big Picture 从网表到版图!

  • Synthesis 综合

  • Floorplanning 地板规划

  • Placement 布局

  • CTS (Clock Tree Synthesis) 时钟树综合:

    • 为什么叫 “树” 呢? 因为时钟信号源 (clock source) 一般只有一个 (时钟引脚或锁相环的输出), 类比为树的根节点; 而时钟信号的接收端 (clock sink) 有很多, 类比为树的叶子节点 [6].
    • 策略:
      • low latency, low skew (时钟信号尽可能同时到达各个 sink), low jitter (低抖动, TODO), high drive (高驱动能力, 通过插入专用的时钟 buffer 来实现, 但是可能会影响 latency 和 skew).

  • Routing 布线

  • Signoff 签核: 确保 GDS 版图是可生产的, 比如检查 [6]:

    • PPA
    • STA (检查能否满足用户指定的频率标准)
    • 信号完整性 (比如分析相邻走线之间的 crosstalk)
    • PV (Physical Verification) 物理验证
      • DRC (Design Rule Check) 设计规则检查: 保证 GDS 版图满足晶圆厂的设计规则 (比如 pitch).
      • ERC (Electrical Rule Check) 电学规则检查: 检查是否存在走线悬空、短路等.
      • LVS (Layout Versus Schematic) 版图与原理图比较: 确认 GDS 版图与最初的网表一致.

  • 后续步骤:

    • 晶圆厂: 拿到 GDS 文件后, 按照文件内容制造出 mask 掩膜, 然后用 mask 批量生产出 wafer, 再把 wafer 切割成一颗颗 die.
    • 封装厂: 晶圆厂将 die 交给封装厂进行封装测试, 得到芯片的成品.
    • 开发板团队: 设计 PCB 板, 并把芯片的成品焊接在上面, 得到最终的开发板.

Placement 布局

三个阶段

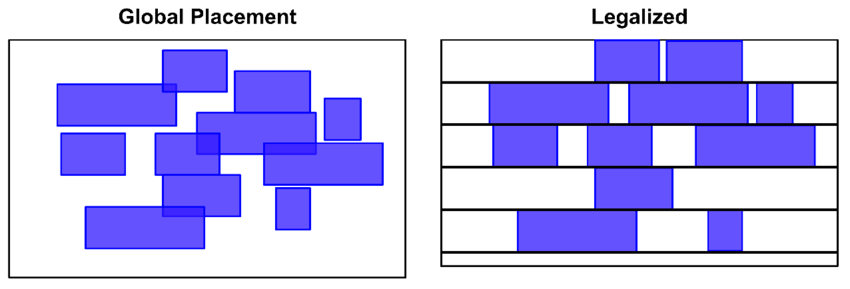
  • Global (coarse/initial) placement: 把 cell/macro 粗略地放置在芯片上的过程 (不必对齐 row/site, 单元之间允许重叠, 但其实会尽量避免重叠) [5].
Figure 4: Legalization 把 cell/macro 吸附到最近的 row/site 上并推开重叠 [5]
Figure 5: Cell/macro 必须放在 row 上 [5].
  • Legalization 合法化: 消除重叠和在两个方向对齐的过程 (见 Figure fig-legalization). Cell/macro 不能随便放置, 而要在 \(x,y\) 方向对齐:
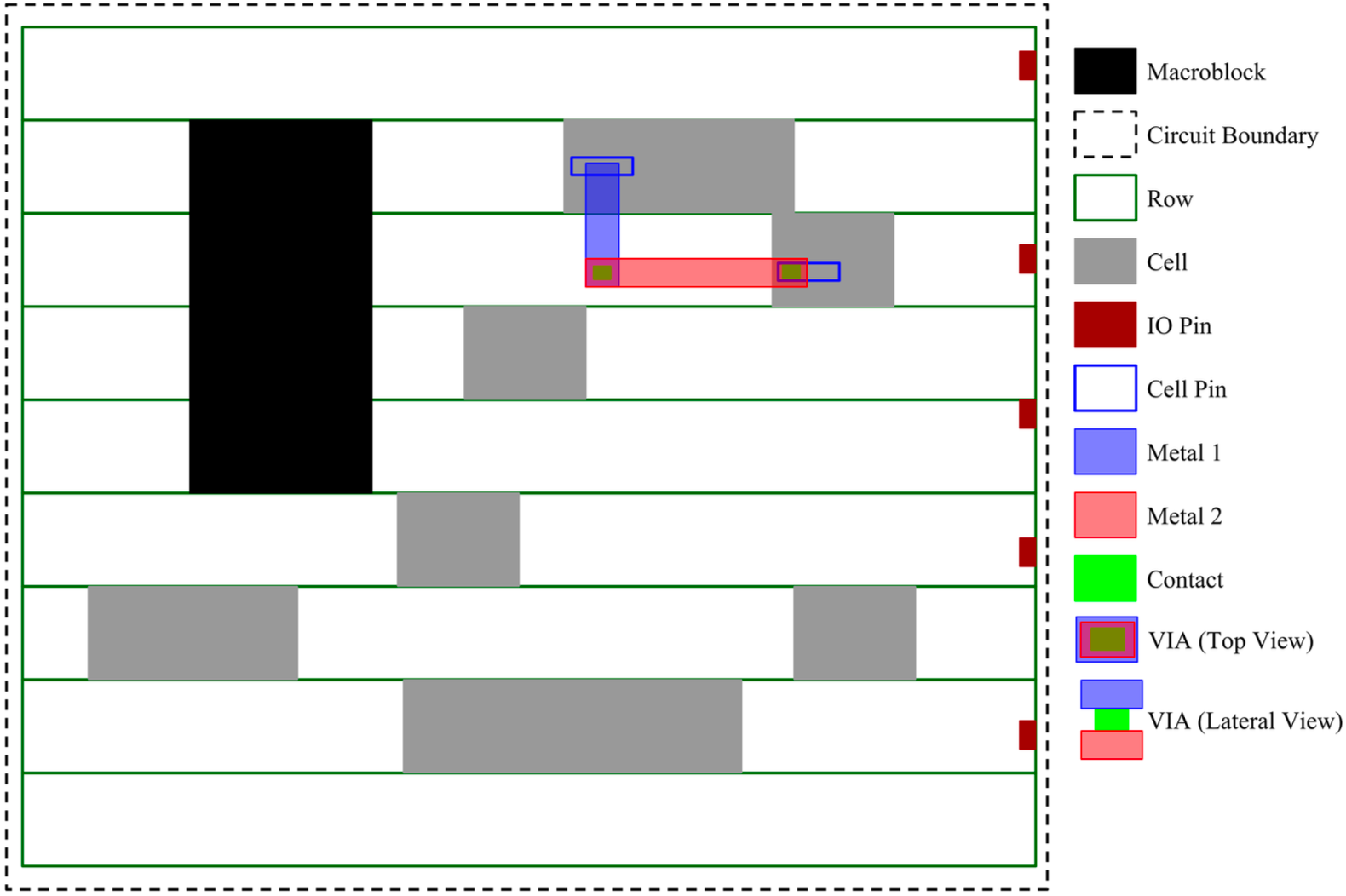
    • Row: 见 Figure fig-layout, 每个 std cell 的上下为该 cell 的供电 metal (上 VDD 下 GND), 我们希望每个 std cell 的这两个 metal 共线, 这样才方便提供统一的供电. 自然的, 所有 cell/macro 要在水平方向成一条线, 使得 die 有“一层一层”的概念, 每一层称为一个 row.
      • Row height 等于 std cell height.
      • Power strip 电源条线: 相邻 Row 的分隔线 (见 Figure fig-sitedemo 的蓝色条), VDD 和 GND 交替.
    • Site: Row 引入了「层」, 而 site 给每一层也数字化引入了「门牌号」, 每个 cell/macro 必须对齐到 row 和 site 边界!
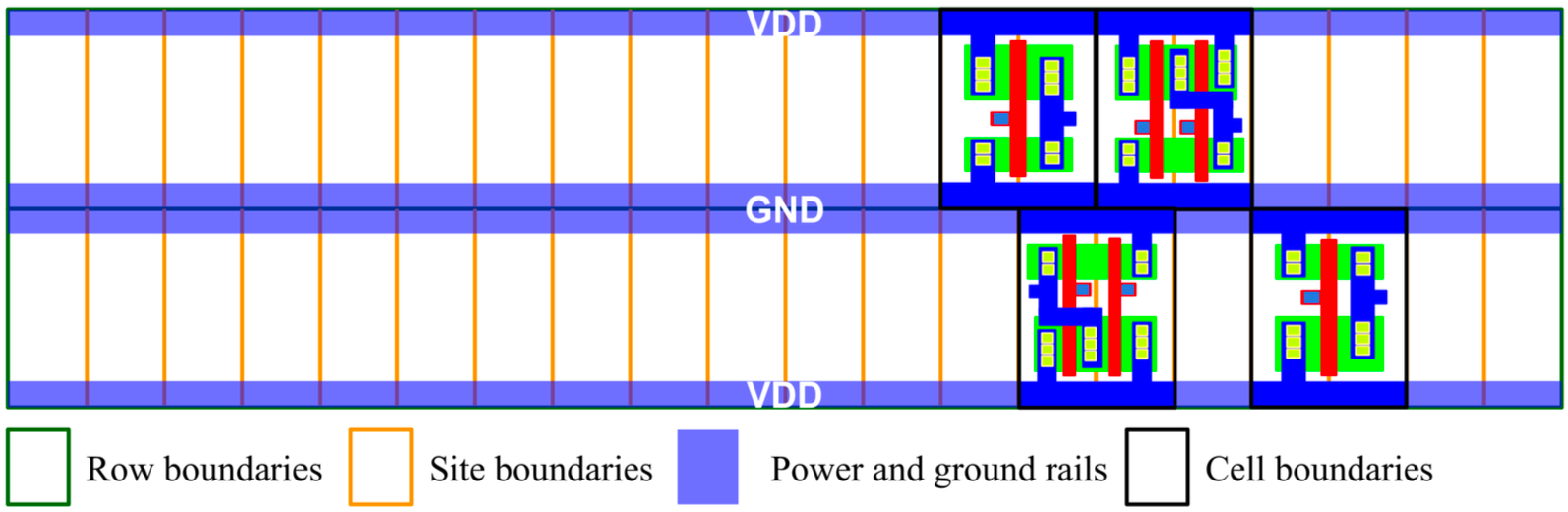
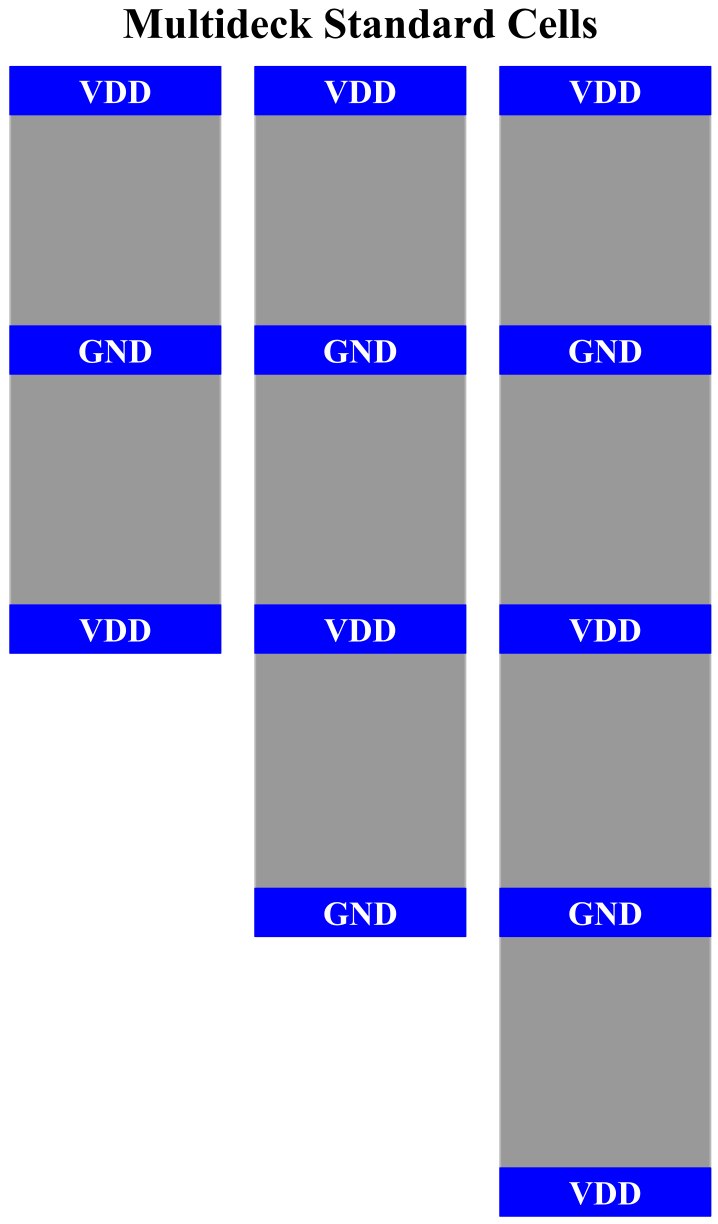
    Figure 6: Std cell 必须上下对齐 row, 左右对齐 site [5]; 且下面一层的 std cell 需要 flip!
  • Detailed placement

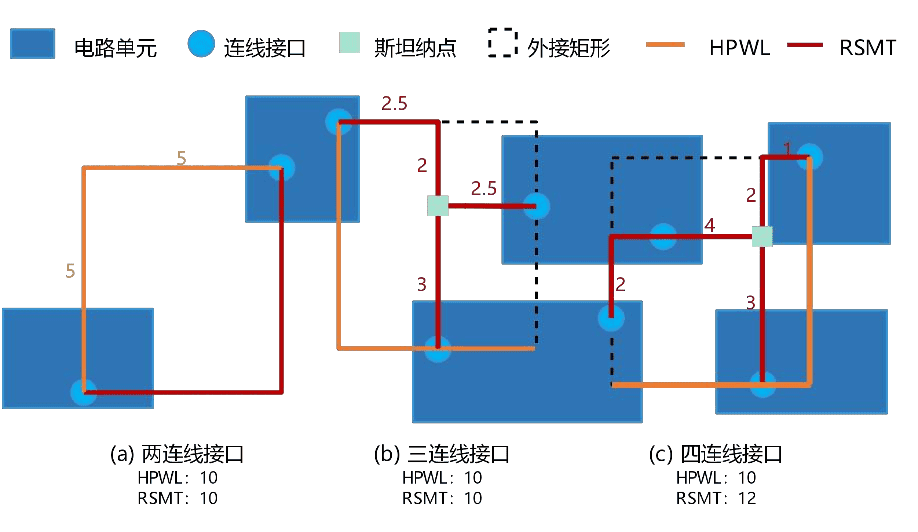
Wirelength Model

Figure 7: 两种估计后续布线时线长的模型: 1. HPWL; 2. 通过构建 RSMT 来计算 [7].

Density Model

  • Bin: 仅仅是为了方便计算3布局的密度 [8] (即有限元方法), 整个 die 被划分为若干个小的矩形区域 (厚度跟 die 的厚度一样), 每个小区域称为一个 bin [3] (见 Figure fig-bindemo). 所有的 bin 组成的集合记作 \(B\).

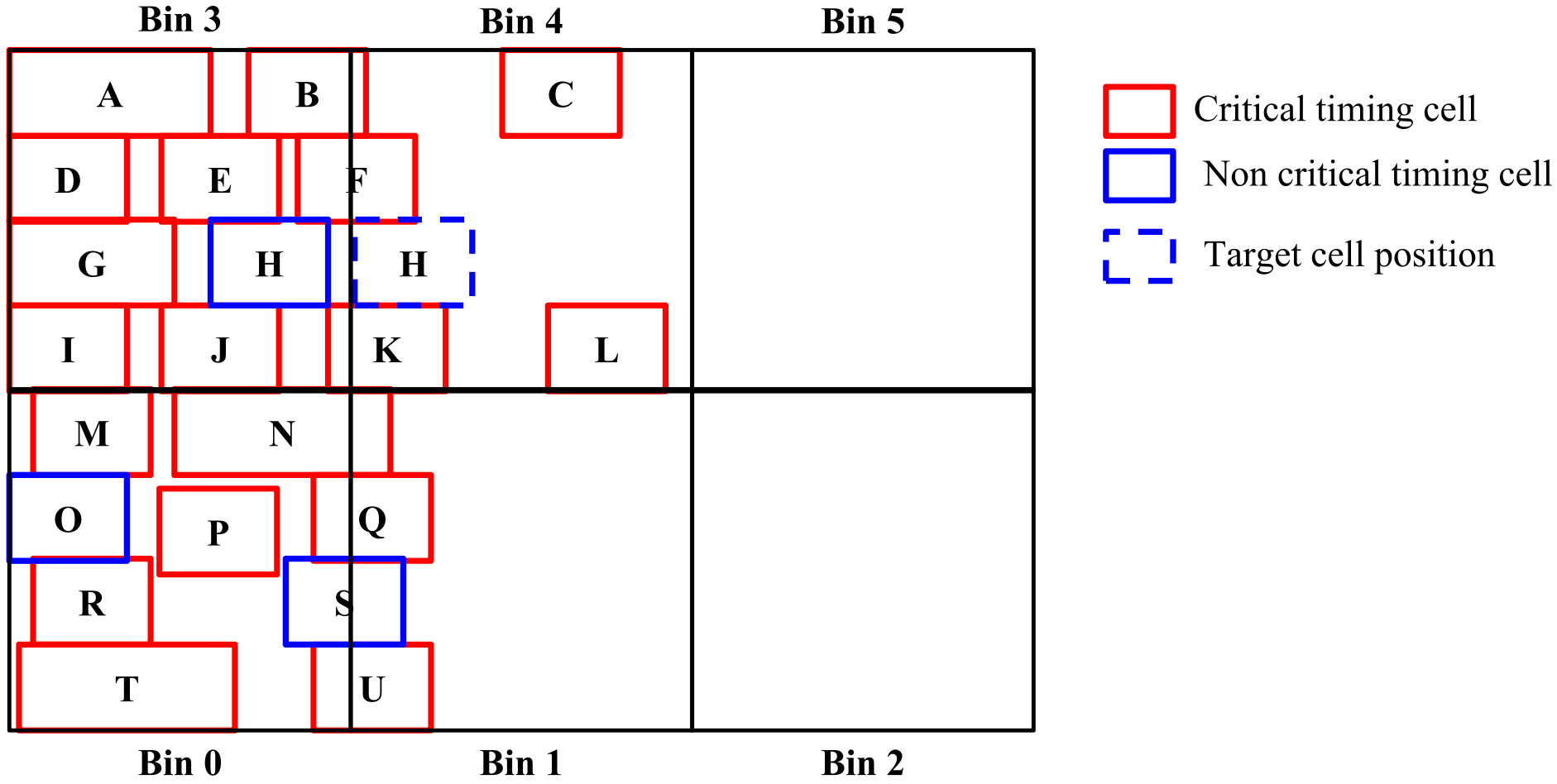
    Figure 8: 此图中 bin 的高度是 row height 的 \(4\) 倍 [5]

3 注意区分 bin 和 row/site 围成的小方格! 前者是为了计算密度而人为划分的区域, 后者是为了放置 cell/macro 而划分的区域.

Timing Model

  • 现在我们还要考虑 slack 的问题 (只考虑 Setup 违规). 由于 slack 跟 wirelength 是有关系的, 将 timing term 与线长解耦是不方便的, 即无法在 Loss function 里单独引入衡量 Timing 的项. [1] 天才般地通过引入 Net weight 这个概念将 timing 的信息融合进 wirelength model 里 (Timing-driven placement).
    • 一个自然的想法是给每个 net 加上权重, 如果一个 net 的 slack 非常负, 说明它的线长急需减小, 那么就给它一个很大的权重. 所以, 可以考虑将 \(-\text{slack}\) 直接作为 net weight.
    • 但是这样实际操作的话会发现优化过程不稳定甚至发散. [1] 文中用了两个貌似 heuristic 的方法来稳定训练过程:
      • 将 \(-\text{slack}\) 作为 net weight 的增量 (而不是直接作为 net weight) ——
      • 也不完全是, 这个增量本身的变化是带动量的 (需要进行历史平滑).
    • 当然我忽略了以下细节 (不重要):
      • 所有量都在 Log scale 下运算.
      • slack 还要先被 WNS normalized 到一个叫 Criticality 的量.
      • 作者还引入了两个超参数 \(\alpha, \eta\) 来调节历史平滑的程度和「小球」的质量大小.

其他优化措施

  • 对标准单元进行镜像对称: 例如某标准单元 A 左侧的端口 p 需要与 A 右侧的另一个标准单元 B 相连, 可以将 A 沿 y 轴进行镜像对称, 使得 p 位于 A 的右侧, 从而让 p 和 B 之间的距离更近. [6]

  • 标准单元过分集中会使得后续布线工作困难, 尽量避免这种情况. [6]

References

[1]
P. Liao, D. Guo, Z. Guo, S. Liu, Y. Lin, and B. Yu, “DREAMPlace 4.0: Timing-driven placement with momentum-based net weighting and lagrangian-based refinement,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 42, pp. 3374–3387, Jan. 2023, doi: 10.1109/tcad.2023.3240132
[2]
P. Liao, Y. Zhao, D. Guo, Y. Lin, and B. Yu, “Analytical die-to-die 3D placement with bistratal wirelength model and GPU acceleration.” 2023. Available: https://arxiv.org/abs/2310.07424
[3]
Y. Zhao, P. Liao, S. Liu, J. Jiang, Y. Lin, and B. Yu, “Analytical heterogeneous die-to-die 3D placement with macros.” 2024. Available: https://arxiv.org/abs/2403.09070
[4]
K. Pingali, “Beyond vertex programs: EDA 3.0.” Sigarch, Dec. 2018. Available: https://www.sigarch.org/beyond-vertex-programs-eda-3-0/. [Accessed: Dec. 06, 2025]
[5]
J. Monteiro, “Algorithms to improve area density utilization, routability and timing during detailed placement and legalization of VLSI circuits,” PhD thesis, 2019.
[6]
Y. videos, “Physical design - from netlist to layout.” Bilibili.com, Nov. 2025. Available: https://www.bilibili.com/video/BV15ZUzBoEf6/?spm_id_from=333.1391.0.0&vd_source=42579e22289b6144ba0b2bdcf99834e3. [Accessed: Jan. 16, 2026]
[7]
iEDA, “A7-VLSI auto placement for circuit cells.” Oscc.cc, Aug. 2024. Available: https://ieda.oscc.cc/en/train/practice/algorithms/a7.html. [Accessed: Dec. 05, 2025]
[8]
iEDA, “8.3 layout problems and modeling.” Oscc.cc, Aug. 2024. Available: https://ieda.oscc.cc/en/train/eda/eda-model/8_3_palcement.html. [Accessed: Dec. 05, 2025]