What is symmetry? 什么是对称性?

Symmetry is nothing but a group acts on an object!

1 Discover Symmetry

You may have noticed these concepts:

1.1 (Additive) Even/Odd Functions

Even/odd complex-valued function

Definition 1 A function \(f: \mathbb{R}^n \to \mathbb{C}\) is called

• conjugate symmetric \(:\iff f(-\mathbf{v}) = \overline{f(\mathbf{v})}, \forall \mathbf{v} \in \mathbb{R}^n\),
• conjugate anti-symmetric \(:\iff -f(-\mathbf{v}) = \overline{f(\mathbf{v})}, \forall \mathbf{v} \in \mathbb{R}^n\)

Special cases of Definition 1

Even/odd real function

Definition 2 A function \(f: \mathbb{R} \to \mathbb{R}\) is called

• even \(:\iff f(-x) = f(x), \forall x \in \mathbb{R}\),
• odd \(:\iff -f(-x) = f(x), \forall x \in \mathbb{R}\)

Even/odd multivariate real function

Definition 3 A function \(f: \mathbb{R}^n \to \mathbb{R}\) is called

• even \(:\iff f(-\mathbf{v}) = f(\mathbf{v}), \forall \mathbf{v} \in \mathbb{R}^n\),
• odd \(:\iff -f(-\mathbf{v}) = f(\mathbf{v}), \forall \mathbf{v} \in \mathbb{R}^n\)

Decomposition Property

Theorem 1 Any function \(f: \mathbb{R}^n \to \mathbb{C}\) can be decomposed¹ into a symmetric part \(Sf\) and a anti-symmetric part \(Af\): \[ f = \frac{Sf + Af}{2}, \] \[ Sf := f(\mathbf{v})+\overline{f(-\mathbf{v})}, \] \[ Af := f(\mathbf{v})-\overline{f(-\mathbf{v})}. \]

In fancier language, \[ \mathbb{C}^{\mathbb{R}^n} = S\mathbb{C}^{\mathbb{R}^n} \oplus A\mathbb{C}^{\mathbb{R}^n}. \]

¹ The reason why I do NOT define \(Sf = (f(\mathbf{v})+\overline{f(-\mathbf{v})})/2\) will be clear later.

Note

As a special case of Theorem 1, any function \(f: \mathbb{R} \to \mathbb{R}\) is a sum of an even and an odd function: \[ f = \frac{(f(x) + f(-x))+(f(x) - f(-x))}{2}. \]

1.2 (Multiplicative) Even/Odd Functions

There are also multiplicative version of Definition 1 and Theorem 1:

Multiplicative version of Definition 1

Definition 4 A function \(f: (\mathbb{R}^{\times})^n \to \mathbb{C}\) is called²

• Multiplicative conjugate symmetric \(:\iff f(\frac{1}{\mathbf{v}}) = \overline{f(\mathbf{v})}, \forall \mathbf{v} \in \mathbb{R}^n\),

• conjugate anti-symmetric \(:\iff \frac{1}{f(\frac{1}{\mathbf{v}})} = \overline{f(\mathbf{v})}, \forall \mathbf{v} \in \mathbb{R}^n,\)

where \(\frac{1}{\mathbf{v}}\) is another vector in \((\mathbb{R}^{\times})^n\) whose components are the reciprocal of those of \(\mathbf{v}\).

² \(\mathbb{R}^{\times} := \mathbb{R} \backslash \{0\}\).

Multiplicative version of Decomposition Property

Theorem 2 Any function \(f: (\mathbb{R}^{\times})^n \to \mathbb{C}\) can be decomposed into a symmetric part \(S^{\bullet}f\) and a anti-symmetric part \(A^{\bullet}f\): \[ f = \sqrt{S^{\bullet}f \cdot A^{\bullet}f}, \] \[ S^{\bullet}f := f(\mathbf{v}) \cdot \overline{f(\mathbf{v}^{-1})}, \] \[ A^{\bullet}f := \frac{f(\mathbf{v})}{\overline{f(\mathbf{v}^{-1})}}. \]

1.3 Symmetric/Alternating Tensor

Symmetric/Alternating Tensor

Definition 5 A symmetric rank-\(k\) tensor \(f: V^k \to \mathbb{R}\) is symmetric iff \[ f(v_{\sigma(1)}, \dots, v_{\sigma(k)}) = f(v_1, \dots, v_k) \] for all permutations \(\sigma \in S_k\).

It is alternating iff \[ f(v_{\sigma(1)}, \dots, v_{\sigma(k)}) = (\operatorname{sgn} \sigma) f(v_1, \dots, v_k) \] for all permutations \(\sigma \in S_k\).

Though generally we cannot decompose an arbitrary tensor into a symmetric and alternating part, we could build them by introducing two operators:

Symmetric/Alternating Operator for Tensors

Definition 6 Given \(\forall f: V^k \to \mathbb{R}\), the operator \(S\) and \(A\) defined below always give a symmetric and alternating tensor³: \[ Sf := \sum_{\sigma \in S_k} \sigma f, \] \[ Af := \sum_{\sigma \in S_k} \operatorname{sgn}(\sigma) \sigma f. \]

³ \(\sigma f\) is defined by \((\sigma f)(v_1, v_2, \ldots, v_k) := f(v_{\sigma(1)}, v_{\sigma(2)}, \ldots, v_{\sigma(k)}).\)

1.4 Matrix

Self-adjoint and Skew-adjoint Matrices

Definition 7 A linear operator \(\phi \in \operatorname{Hom}(V)\) is called self-adjoint iff \[ \phi^H = \phi, \] and skew-adjoint iff \[ \phi^H = -\phi. \]

2 Symmetry as Group Action

2.1 Problem

Is there any way to unify these seemingly “symmetric” concepts? What kind of mathematical object can be symmetrize and and alternate? When does the object itself expressible by only its symmetrized and and alternated ones?

2.2 Important Observation

The common thing of the above examples in Section 1 is that the domain of the objects (functions, tensors, matrices⁴) could be manipulated by some kind of actions:

⁴ This is left as an exercise.

• \(f: \mathbb{R}^n \to \mathbb{C}\): additive inversion,
• \(f: (\mathbb{R}^{\times})^n \to \mathbb{C}\): multiplicative inversion,
• \(f: V^k \to \mathbb{R}\): permutation.

The first two can be viewed as the 2-element group \(S_2\) acts on the domain of \(f\), where \(S_2\) is the group generated by the operation of “taking inverse”: \[ S_2 := \langle\cdot^{-1}\rangle = \{e, \cdot^{-1}\}, \] or equivalently, the permutation group on two letters: \[ S_2 = \{e, (12)\}. \]

Therefore, in the first two cases, we could define a \(S_2\)-action: \[ (\sigma f)(\mathbf{v}) := \overline{f(\mathbf{v}^{-1})}, \] where \(\mathbf{v}^{-1}\) is either \(-\mathbf{v}\) (additive inverse) or \(1/\mathbf{v}\) (multiplicative inverse).

Therefore, the definition of the operator \(S\) and \(A\) in Definition 6 also applies for the first two cases: \[ Sf := \sum_{\sigma \in S_2} \sigma f = f(\mathbf{v}) + \overline{f(-\mathbf{v})} \quad (\text{or } f(\mathbf{v})\cdot \overline{f(-\mathbf{v})}), \] \[ Af := \sum_{\sigma \in S_k} \operatorname{sgn}(\sigma) \sigma f = f(\mathbf{v}) - \overline{f(-\mathbf{v})} \quad (\text{or } \frac{f(\mathbf{v})}{\overline{f(\mathbf{v}^{-1})}}). \]

2.3 When Decomposable?

In the first two cases, \(f\) can be expressed purely by \(Sf\) and \(Af\): \[ f = \frac{Sf + Af}{2} \quad (\text{or } \sqrt{Sf \cdot Af}), \] which is just the average of them! (Arithmetic average and geometric average respectively)

But we don’t have this relationship for tensors, i.e., not every rank \(k\) tensor can be purely expressed using \(Sf\) and \(Af\) – apart from the case when \(k = 2\): \[ f(v_1, v_2) = \frac{(f(v_1, v_2)+f(v_2, v_1))+(f(v_1, v_2)-f(v_2, v_1))}{2} = \frac{Sf + Af}{2}. \]

What happened when \(k \ge 3\)?

Let \(f: V^3 \to \mathbb{R}\), we have \[ Sf = f(v_1, v_2, v_3) + f(v_2, v_3, v_1) + f(v_3, v_1, v_2) + f(v_2, v_1, v_3) + f(v_1, v_3, v_2) + f(v_3, v_2, v_1), \] \[ Af = f(v_1, v_2, v_3) + f(v_2, v_3, v_1) + f(v_3, v_1, v_2) - f(v_2, v_1, v_3) - f(v_1, v_3, v_2) - f(v_3, v_2, v_1). \]

Visualize group action

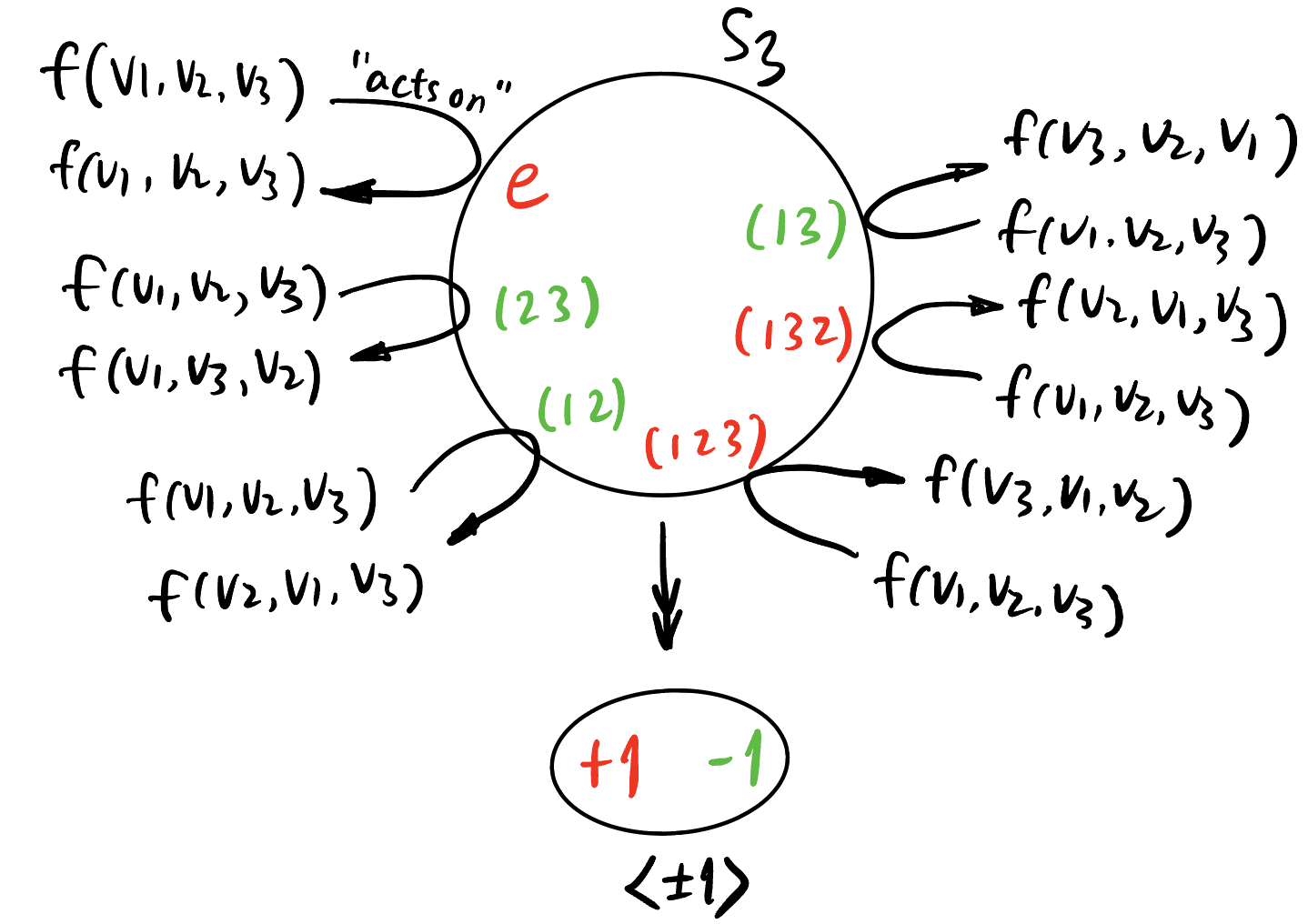
The result \[ \frac{Sf + Af}{2} = f(v_1, v_2, v_3) + f(v_2, v_3, v_1) + f(v_3, v_1, v_2) = \sum_{\sigma \in A_3} \sigma f \neq f, \] where \(A_3\) is the alternating group (the group of even permutations) on three letters.

2.4 Try Yourself!

Exercise 1 (\(S\) and \(A\) operator for matrices \(\phi\)) Let \(\phi \in \operatorname{End} (\mathbb{C}^n)\), derive the definition of \(S\phi\) and \(A \phi\).

Solution

\[ S \phi := \frac{\phi + \phi^H}{2}, \] \[ A \phi := \frac{\phi - \phi^H}{2}. \]

We also have \[ \phi = \frac{S \phi + A \phi}{2}. \]