DSP Crash Course 数字信号处理速成笔记

Crash-Course
CN-blogs
(已停更 Jul 2, 10:53, 2025)
Author

Marcobisky

Published

June 29, 2025

本笔记是本人电子科技大学格院大三《数字信号处理》课程的期末考试复习笔记, 遵循个人学习习惯与轨迹, 不保证严谨性和绝对正确性.

1 FFT 快速傅里叶变换

2 Fourier Transform 傅里叶变换

3 Complex Analysis Basics 复变函数基础

4 \(\mathcal{Z}\) 变换, \(\mathcal{L}\) 变换

在傅立叶分析中我们用 线性空间和内积 的思维框架来处理信号, 但是在 \(\mathcal{Z}\) 变换和 \(\mathcal{L}\) 变换中, 一般用 级数 来思考.

4.1 动机: 复频率的引入

动机很重要, 它决定了今后你对 \(\mathcal{Z}\) 变换和 \(\mathcal{L}\) 变换的 Mental picture.

\(\mathcal{Z}\) 变换和 \(\mathcal{L}\) 变换初看有点不自然, 是因为复频率的引入经历了以下几个重要的数学思想:

  • 不妨都在复数域上看一看: 这导致了 Complexification 复化 (见 EM Crash Course) 这个概念. 这将从 “研究复信号的实部” 到 “研究复信号本身”.

  • 复频率的引入: 由于指数信号和正弦信号都长这样 \(e^{s t}\) (\(s\) 是实数或纯虚数的区别), 我们发现指数增长和振荡的本质在复信号看来是一样的, 干脆让 \(s\) 为复数, 它的:

    • 实部 \(\Re(s)\) 代表指数增长
    • 虚部 \(\Im(s)\) 代表振荡

    称 \(x(t)\) 在 \(e^{s t}\) 基上的 Fourier 变换为 Laplace 变换. (要注意内积的话要取共轭 \(e^{-st}\))

  • 动机: 我们可以将「频率 \(\omega\)」这个概念推广到 \(\mathbb{C}\) 上!

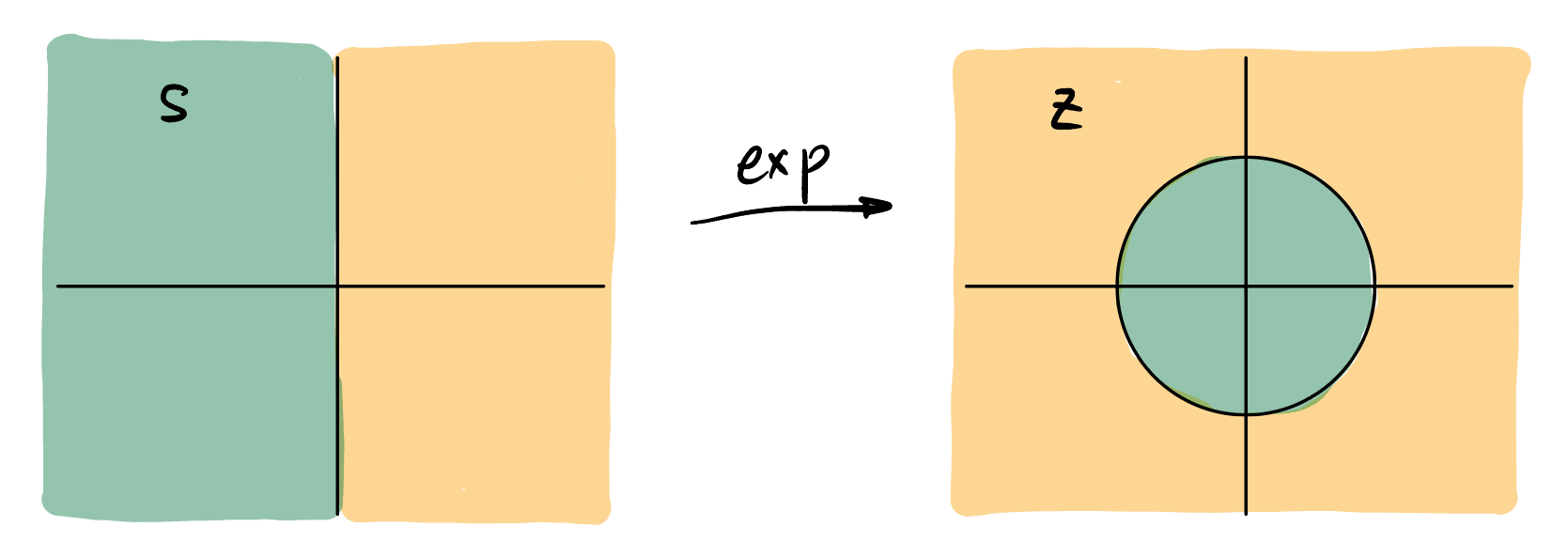
    • 如果是离散时间信号, 频率一定限制在 \([0, 2\pi]\) 之间, 一个很自然的想法是用一个复数 \(z\) 的:
      • 角度 \(\omega\) 来表示频率
      • 模长 \(r\) 来表示指数衰减
      所以

  • \(\mathcal{Z}\)-Transform: 我们可以将每一个离散时间信号 \(x[n]\) 都对应一个复变函数 \(X(z)\): \[ X(z) := \sum_{n=-\infty}^{+\infty} x[n] z^{-n}. \tag{1}\] 即将 \(x[n]\) 作为一个 Laurent 级数的系数. 称 \(X(z)\) 为 \(x[n]\) 的 \(\mathcal{Z}\) 变换.

    • 使 Equation 1 收敛的 \(z\) 的集合称为 ROC (收敛域).
    • 任何一个复变函数1 \(X(z)\) 在单位圆上的取值即为 其 Laurent 级数的系数 Fourier 变换的结果.
    • 由对偶性知: 任何一个复变函数 \(X(z)\) 在单位圆上取值的 Fourier 变换的结果即为 其 Laurent 级数的系数.

1 这个复变函数应该在包含单位圆的一个 Annulus 上解析 (holomorphic).

  • \(\mathcal{L}\)-Transform: 多一个对数映射, 单位圆变成了虚轴: \[ X(s) := \int_{-\infty}^{+\infty} x(t) e^{-st} dt. \tag{2}\]

    • 使 Equation 2 收敛的 \(s\) 的集合称为 ROC (收敛域).
    • \(X(s)\) 在虚轴上的取值即为 \(x(t)\) 的 Fourier 变换的结果.

    \(z = e^s\)
Code 
import {PlotContext, ComplexVariable, DomainColoringLayer, glslFunctionMapping} from "39fe342decb60c30"

viewof expr = Inputs.text({
    label: "Function f(z)=",
    value: "(z-0.5)*(z+0.7)/((z+0.4*i)*(z-0.4*i))",
    placeholder: "e.g. (z-i)/(z+1)"
})

domainColoringConfig = ({
    phaseColoring: 1,
    phaseShading: 0,
    magnitudeShading: 0
})

plot = PlotContext({
    xrange: [-1.4, 1.4],
    yrange: [-1.2, 1.2],
    width: 0.7*width,
    height: Math.max(400, Math.floor(width * 0.4))
})

plot([DomainColoringLayer(expr, "z", domainColoringConfig)])

4.2 ROC (Region of Convergence) 收敛域

  • 关键信息:

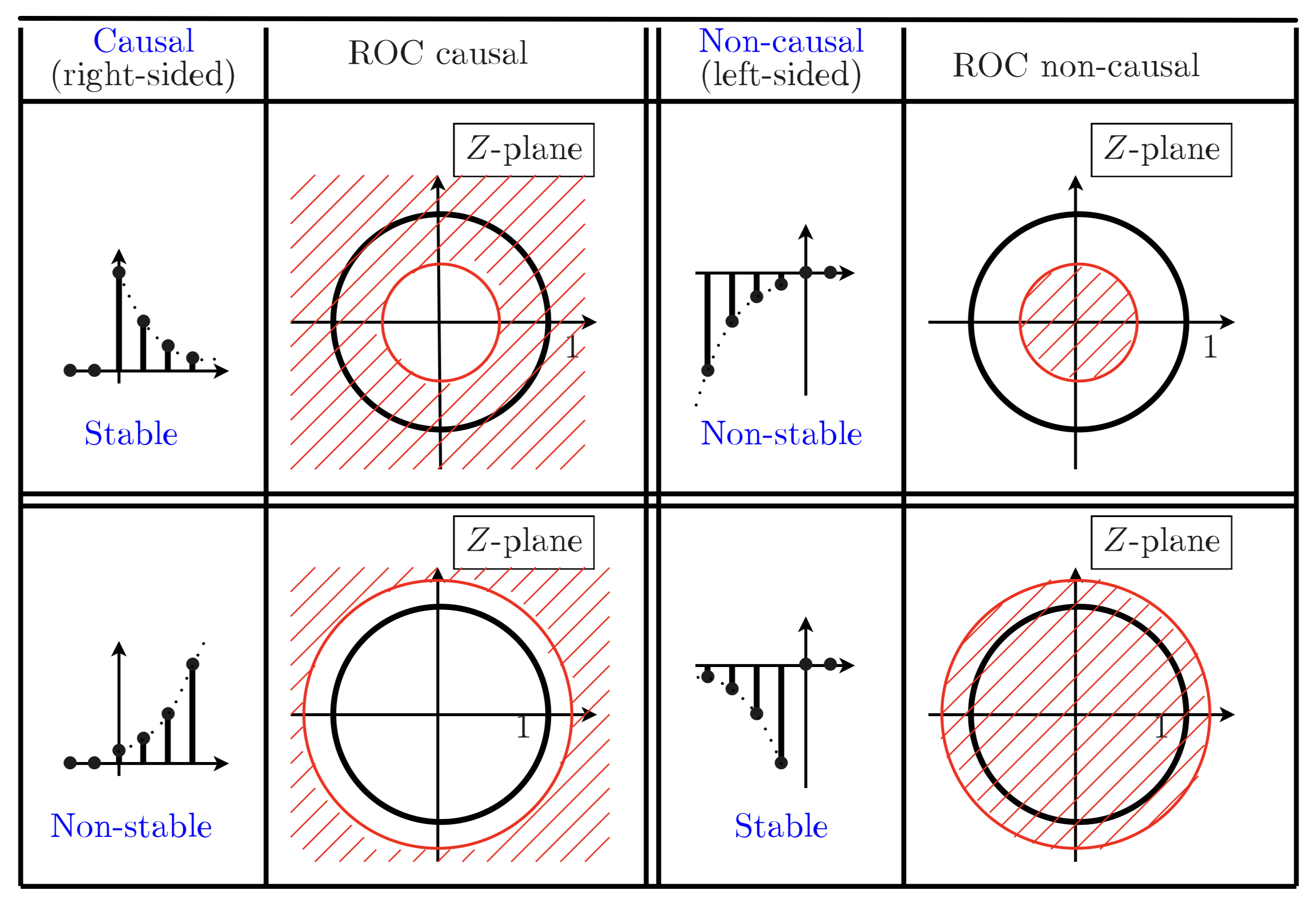
    • 包不包含单位圆: 包含 -> BIBO Stable
    • 向外还是向内:
      • 外 -> Right-sided
      • 内 -> Left-sided
      • 环 -> Finite-length
    • Causal 是 Right-sided 的特例, 仅看 ROC 不能判断 causal.

  • \(s\) 平面右侧 和 \(z\) 平面圆外 为 原信号乘上衰减的指数信号后 Fourier 变换的结果.

  • \(s\) 平面左侧 和 \(z\) 平面圆内 为 原信号乘上增长的指数信号后 Fourier 变换的结果.

  • ROC 的边界一定有 pole! ROC 的内部一定不包含 pole!

    \(z\) 平面的 ROC

5 Transfer Function 的分类

5.1 Time 时间上

  • FIR
  • IIR

5.2 Freq 频域上

  • 幅度 \(|H|\):
    • 理想滤波器: Passband, Stopband (涉及的概念)
    • BR (Bounded Real): 因果、稳定、实系数系统, \(|H| \leq 1\), 由 Parseval’s 定理知: 能量减少 $ |Y|^2 |X|^2 $ Passive structure.
    • LBR (Lossless BR): 因果、稳定、实系数系统, \(|H| = 1\). 能量无损耗.
    • All pass 全通: 仅仅是 \(|H| = 1, \forall \omega\).
      • Mirror-image Polynomial 镜像多项式: 比如以下两个多项式互为镜像:\[\begin{aligned}D_3(z) &= 1 + 2z^{-1} + 3z^{-2} + 4z^{-3} \\ D_3^{\circ}(z) &= 4 + 3z^{-1} + 2z^{-2} + z^{-3} \end{aligned}\]
      • 实系统 \(H(z) = \frac{B(z)}{A(z)}\) all-pass \(\iff\) \(B(z)\) 与 \(A(z)\) 互为镜像.

我们知道对于实系统 \(H(e^{j \omega})\), \[ H^*(e^{j \omega}) = H(e^{-j \omega}). \]

  • 相位 \(\angle H\):

    • Group Delay 群延迟: \(\omega\) 的频率成分通过系统后延迟了多少秒. 反过来思考, 我们知道延迟 \(\tau\) 会导致不同的频点有不同的相位变化 (乘了 \(e^{-j\omega \tau}\)), 相位变化为 \(-\omega \tau\). 那对于一般的系统, 在频点 \(\omega\) 的相位变化就是 \(\angle H(\omega)\), 如何从中获取 \(\tau\)? \[ \tau_g (\omega) = - \frac{\mathrm{d} (-\omega \tau)}{\mathrm{d} \omega} = \frac{\mathrm{d} \angle H(\omega)}{\mathrm{d} \omega}. \]
    • Zero-Phase 零相位系统: \(H \in \mathbb{R}\) 且 \(|H| \ge 0\). 注意幅值也要非负! 对因果系统不存在??
    • Linear-Phase 线性相位系统: 就是时域延迟系统 (群延迟为常数), i.e., 波通过系统后在 \(\omega\) 频点上的相位变化 \(\propto \omega\), 正比系数就是 \(\tau\), 表现为信号延迟了 \(\tau\) 秒.
    • Minimum Phase 最小相位系统: \(H\) 的 zeros 都在单位圆内.
    • Maximum Phase 最大相位系统: \(H\) 的 zeros 都在单位圆外.
    • Mixed Phase 混合相位系统: \(H\) 的 zeros 在单位圆内外都有.

6 Digital Filter 数字滤波器

  • dB 分贝: 人类的构造决定了感知物理量 (声音、光强等) 是对数的, 我们引入 dB 分贝: \[ (-) \quad 10 \lg |H|^2. \]

    • \(10\) 表示 d, 平方表示功率.
    • 放大 \(-0.1 \text{ dB}\) 也称 attenuate \(0.1 \text{ dB}\), 包含负号.

6.1 Characteristics 数字滤波器指标

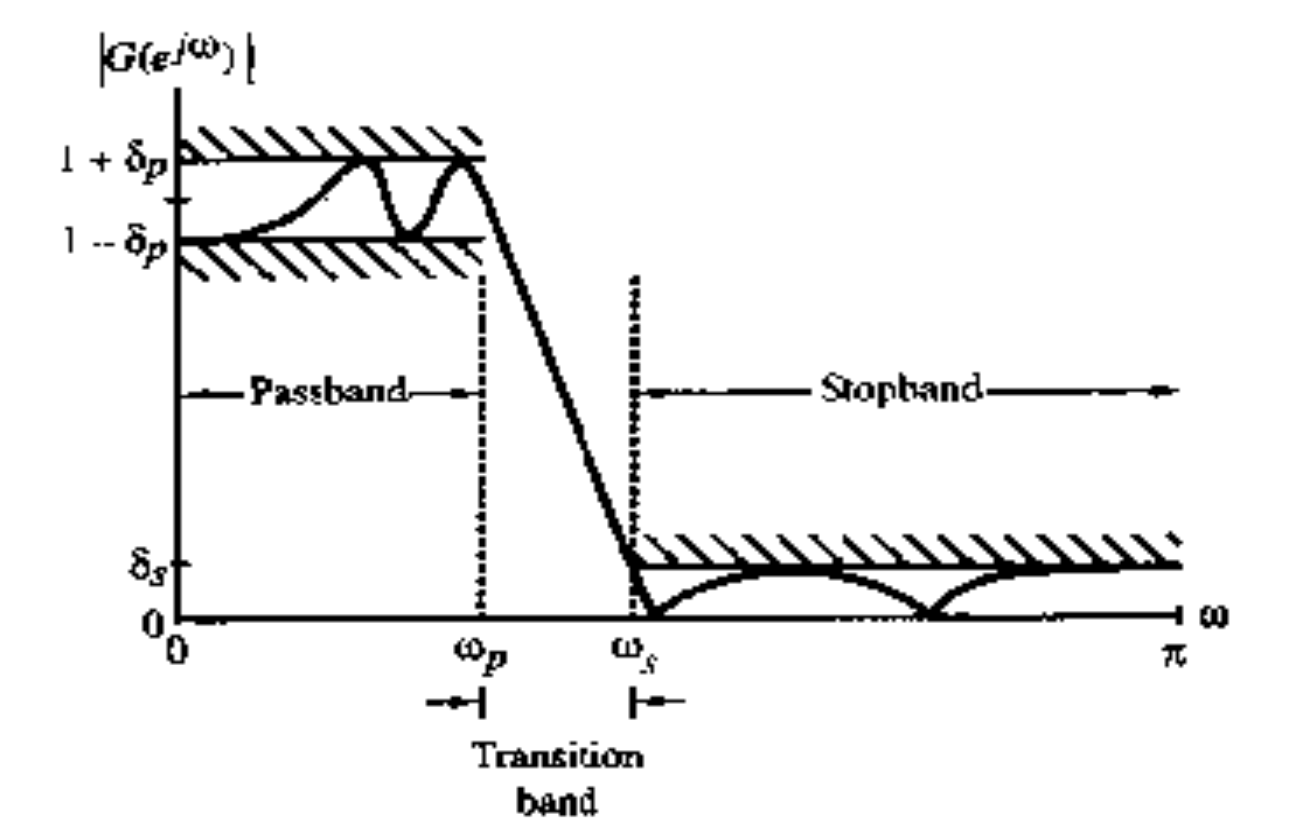
以 LPF 为例, 关键参数:

  • Tolerance 容差: \(\delta_p, \delta_s\).
  • Edge Frequency 边界频率: \(\omega_p, \omega_s\).
    • 若不在 \([0, \pi]\) 内, 则需要 数字归一化: \(\omega_p = 2\pi \frac{F_p}{F_{\text{sample}}}.\)

Let the specified passband and stopband edge frequencies of a digital highpass filter operating at a sampling rate of \(25 \text{ kHz}\) be \(7 \text{ kHz}\) and \(3 \text{ kHz}\), respectively. We determine the corresponding band edge frequencies of the digital filter: \[ \omega_p = \frac{2\pi (7 \times 10^3)}{25 \times 10^3} = 0.56\pi, \quad \omega_s = \frac{2\pi (3 \times 10^3)}{25 \times 10^3} = 0.24\pi. \]

  • Peak Passband Ripple 峰值通带波纹: \(\boxed{\alpha_p = -20 \lg (1- \delta_p)}\), 越小越好.

  • Minimum Stopband Attenuation 最小阻带衰减: \(\boxed{\alpha_s = -20 \lg \delta_s}\), 越大越好.

    Characteristics of a LPF

6.2 Design 数字滤波器设计

  • Objective: 设计出来的必须是 causal 和 stable 的. IIR 和 FIR 的优缺点:
    • IIR: 一般 lower order, 计算复杂度低, 但要确保稳定. 可想象成反馈系统.
    • FIR: 一般 higher order, 计算复杂度高, 一定稳定. 可想象成开环系统.

6.2.1 IIR 数字滤波器设计

  • 步骤
    • Convert the digital filter specifications into analog lowpass prototype one. (因为 analog filter 的设计方法有很多表可以查, 更成熟)
    • Determine the analog lowpass filter \(H_a(s)\) meeting these specifications.
    • Transform it into the desired digital filter transfer function \(G(z)\). (涉及到 \(s\) 域到 \(z\) 域的变换)
      • Impulse Invariance Method 脉冲不变法: 数字系统的冲激响应是模拟系统冲激响应在采样点处的取值. (会发生混叠 aliasing)

      EXAMPLE: 脉冲不变法举例
      • Bilinear Transformation 双线性变换: